Назовем треугольник АВС.
Если провести перпендикуляр ВН, образуется два треугольникаАВН и ВНС. В равностороннем тр все стороны равны и углы по 60градусов. Тогда в одном из образовавшихся треугольников видим, что поделенное основание( половина его) равно половине гипотенузы, потому что сторона, лежащая напротив угла в тридцать градусов равна половине гипотенузы. Поэтому АН равен половине АВ, он лежит напротив угла АВН=30гр.
АН=х АВ=2х
Запишем уравнение:
По теореме Пифагора найдем х: x^2+12^2=(2x)^2
48=x^2
x=корень из48
сторона будет равна 2корня из 48, потому что АН=НС, высота поделила сторону напополам!
АС=АВ=ВС=2корень из48
S= 12*2корень из48/2= 12корень из48. одного треугольника.
Чтобы найти площадь треугольника, образованного сторонами-мелианами, нарисуем треугольник побольше, его стороны будут лежать за пределами маленького треугольника и в центрах высот углов маленького треугольника. Данная фигура образует 4 одинаковых треугольника, поэтому площадь фигуры равна:
Площадь всей фигуры равна 4*s
=4*12корень из48=48корень из48. ответ:48корней из 48.
Точно такую задачу уже решала. Даю ее подробное решение .
В треугольнике АВС угол В равен 120°, а длина стороны АВ на 7√3 меньше
полупериметра треугольника.
Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС.
-------------------------------------------------------------------------------------------------------------------
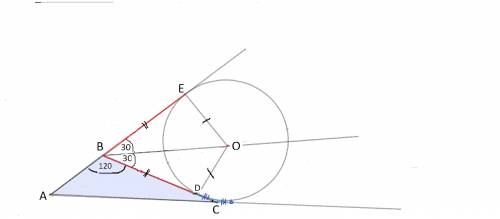
Сделаем рисунок.
Окружность, радиус которой нужно найти - вневписанная.
В любом треугольнике
расстояние от вершины треугольника до точки касания вневписанной окружности (касающейся противоположной данной вершине стороны треугольника и продолжений двух других его сторон) с продолжением стороны треугольника, выходящей из данной вершины, есть полупериметр треугольника.
( Доказательство этой теоремы при желании легко найти, в данном случае оно не является целью решения)
То-есть в данной задаче AЕ = p.
Вневписанная окружность касается стороны ВC треугольника ABC, отрезки касательных от вершины А до точек касания с вневписанной окружностью равны полупериметру треугольника.
Это утверждение вытекает из того, что
по свойству отрезков касательных из точки вне окружности отрезки от В до точек касания равны, равны и отрезки от С до точек касания. Сумма их с соответствующими сторонами треугольника является его полупериметром.
Центр данной окружности лежит на биссектрисе угла СВЕ.
Так как этот угол смежный с углом АВС,
он равен 60°, а угол ОВЕ=30°.
Так как длина стороны АВ на 7√3 меньше полупериметра треугольника, а АЕ - равна полупериметру, то
ВЕ=7√3
Радиус ОЕ:ВЕ= tg (30°) = 1/√3
Радиус ОЕ:ВЕ=R:7√3
R:7√3 = 1/√3
R=7√3 ·1/√3=7
Відповідь:
я не понимаю
Пояснення: