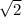
Периметр прямоугольника равен удвоенной сумме двух его смежных сторон. P = 2(AB+BC),
BC = BK + KC = 8 см + 5 см = 13 см.
AK — биссектрисса угла A, угол BAK = угол KAD = 90°÷2 = 45°,
Рассмотрим треугольник ABK. Сумма углов треугольника равна 180°. угол BKA = 180° – угол ABK – угол BAK = 180° – 90° – 45° = 45°, угол BKA = угол BAK, углы при основании равны, треугольник — равнобедренный, значит боковые стороны равны, AB = BK = 8см.
P = 2(AB + BC) = 2(8см + 13см) = 2 × 21 см = 42 см.
ответ: 42 см
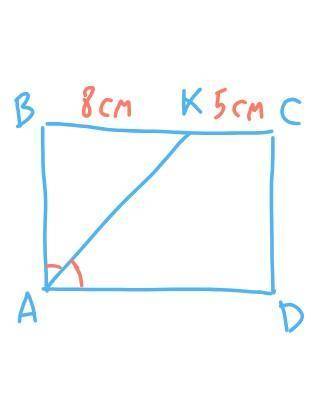

для вписанной окружности:
центр ---пересечение биссектрис углов треугольника
т.к. одна из биссектрис (проведенная к основанию (а)) ---медиана и высота, можно записать по определению тангенса: r / (a/2) = tg(альфа/2)
r = (a/2) * tg(альфа/2)
для описанной окружности: R = a / (2sin(180-2альфа)) = a / (2sin(2альфа))
r/R = a * tg(альфа/2) * 2sin(2альфа) / (2*a) = sin(2альфа)*tg(альфа/2)
можно еще немного сократить...
sin(2a) = 2sin(a)*cos(a) = 4sin(a/2)*cos(a/2)*cos(a)
r/R = 4cos(a)*(sin(a/2))^2 (здесь а---угол альфа)
===============================
Объяснение: