ответ:9 задание:
OM = ON как радиусы окружности. Радиус перпендикулярен касательной, проведенный в его точку касания, значит
угол MKN=360градусов-120градусов-180градусов=60градусов
У прямоугольных треугольников OMK и ONK гипотенуза OK общая и катеты OM=ON, значит эти треугольники равны по катету и гипотенузе. У равных треугольников соответствующие элементы (стороны, углы) равны
MK=KN,OKM=OKN отсюда следует, что OK - биссектриса угла MKN, значитOKM=OKN=30 градусов
KN=MK=OK\cos 30градусов=6*3(в корне)/2=3корень3
10 задание:
BM²=OM²-BO²=
корень900 - 400 =корень500= 10корень5
r(BO)=20
BO=AO=20
AM=30-20=10
Объяснение:
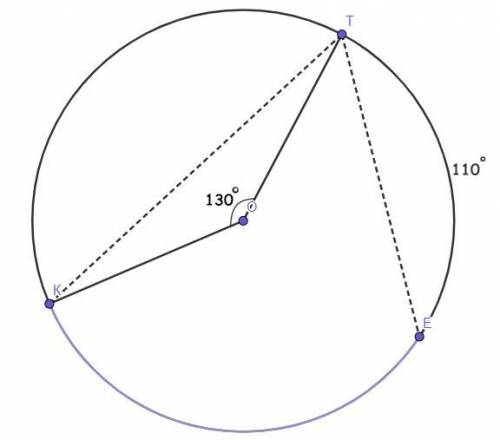
Окружность.
Точка О - центр данной окружности.
Отрезки КТ и ТЕ - хорды.
∠КОТ = 130°.
∪ТЕ = 110°.
Найти :∪КЕ (фиолетовой) = ?
Решение :∠КОТ - центральный (по определению центрального угла).
Градусная мера дуги, на которую опирается центральный угол, равен градусной мере соответствующего центрального угла.Следовательно -
∪КТ = ∠КОТ = 130°.
Сумма дуг с общими концами равна 360°.Следовательно -
∪КЕ (фиолетовая) + ∪КТ + ∪ТЕ = 360°
∪КЕ (фиолетовая) = 360° - ∪КТ - ∪ТЕ
∪КЕ (фиолетовая) = 360° - 130° - 110°
∪КЕ (фиолетовая) = 120°.
ответ :120°.
Пусть В - начало координат.
ВС - ось Х
ВD - ось У
ВВ1 - ось Z
Уравнение плоскости
ВВ1DD1
x-y = 0
Нормаль n (1;-1;0)
Вектор
АМ ( 1/3;0;1)
Синус искомого угла
| AM * n | / | AM | / | n | =
1/3 / √ ( (1/3)^2 +1^2) / √ (1^2+1^2) =
1 / √10 / √2 = 1/ (2√5) = √5/10