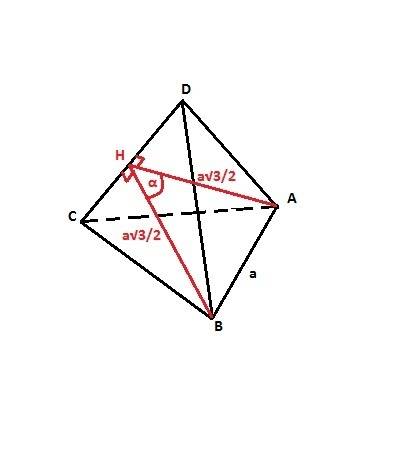
Правильный тетраэдр - это правильная треугольная пирамида у которой все грани являются равносторонними треугольниками. Искомый угол - это угол между высотами двух соседних граней (по определению), то есть это угол при вершине равнобедренного треугольника с боковыми сторонами - высотами граней и основанием - стороной основания тетраэдра. Высота правильного треугольника равна h=(√3/2)*a, где а - сторона треугольника. Тогда по теореме косинусов: Cosα = (AH+BH²-AB²)/(2*AH*BH) или в нашем случае
Cosα =(1/2)*а²/((1/2)*3а²) = 1/3.
ответ: α = arccos(1/3) ≈ 70,5°.
Проведём вторую диагональ BD квадрата ABCD.
По условию AM = MO = ON = NC. Отсюда АО = ОС
Диагонали квадрата равны, взаимно перпендикулярны, и точкой пересечения делятся пополам => AC перпендикулярен BD.
Диагональ BD проходит через середину первой диагонали, то есть через точку О.
Значит, MN перпендикулярен BD
МО = ОN , BO = OD
Диагонали данного четырехугольника ВMDN взаимно перпендикулярны и точкой пересечения делятся пополам. Из этого следует, что четырехугольник ВMDN является ромбом, что и требовалось доказать.