Объяснение:
1.
Дано: ΔАВС.
АВ = ВС;
ВЕ - медиана;
∠АВЕ = 44°
Найти: ∠АВС; ∠FEC.
Рассмотрим ΔАВС.
АВ = ВС ⇒ ΔАВС - равнобедренный.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.⇒ ВЕ - высота и биссектриса.
∠АВЕ = ∠ЕВС = 44° (ВЕ - биссектриса)
⇒ ∠АВС = ∠АВЕ + ∠ЕВС = 44° + 44° = 88°
BF ⊥ АС (ВЕ - высота)
⇒ ∠FEC = 90°
2.
Дано: ΔАВС.
АВ = ВС; АО = ОС;
ОК - биссектриса.
Найти: ∠АОК.
Рассмотрим ΔАВС.
АВ = ВС ⇒ ΔАВС - равнобедренный.
АО = ОС ⇒ ВО - медиана.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.⇒ ВО - высота, то есть ∠ВОС = 90°.
ОК - биссектриса ⇒ ∠ВОК = ∠КОС = 90° : 2 = 45°
∠АОК = ∠АОВ + ∠ВОК = 90° + 45° = 135°
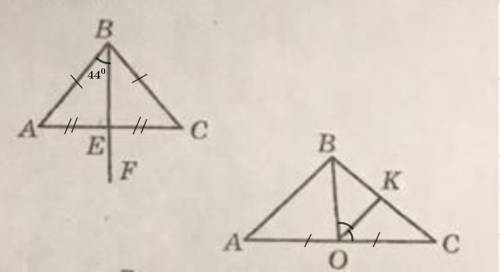
Объяснение:
ABCD - трапеция АВ=СD
BC=4
<A=60 градусов
Вписана окружность
Найти :S
S=4r^2/sinA
Биссектрисы углов при боковой стороне пересекаются под прямым углом :
<АОВ =90 градусов
Сумма углов прилежащих к боковой стороне равна 180 градусов :
<АВС=180-<ВАD=180-60=120 гродусов
Тр-к ВОН:
<BHO=90 градусов (т. к НМ - высота =
=диаметру)
<ОВН=<АВС:2=120:2=60 градусов(т. к ВО - биссектриса)
ВН=ВС:2=4:2=2
tg<OBH=HO/BH
HO=BH×tg60=2корень3
r=HO=2корень3
S=4r^2 / sin<A
=(4×(2корень3)^2) : sin60=
=(4×4×3) : (корень3 /2)=
=48×2/корень3=
=96×корень3 /(корень3 ×корень3) =
=32корень3
ответ : S=32корень3