16
Объяснение: по теореме Пифагора а²+b²=c² <-гипотенуза a²=c²-b²
a²= 20²-12²=400-144=256
a=✓256=16
Через две параллельные прямые можно провести плоскость и при том только одну. Таким образом, точки A, B, C и D лежат в одной плоскости. Плоскость, проходящая через точки B и C, пересекает плоскость ABCD по прямой BC и точка E, принадлежащая отрезку AD, также лежит в плоскости ABCD. Треугольники CDE и ВАЕ, лежащие в одной плоскости, подобны по двум углам, так как АВ параллельна CD (дано) и <CDA=<BAD, как накрест лежащие при параллельных АВ и CD и секущей AD, а <AEB=<CED, как вертикальные.
Коэффициент подобия треугольников равен CD/AB = 6/8 = 3/4.
Тогда СЕ/ВЕ=3/4 => CE = 6*3/4 =4,5.
ED/AE=3/4 => AE=3*4/3 = 4.
AD=AE+ED = 7 ед.
BC=BE+CE = 10,5 ед.
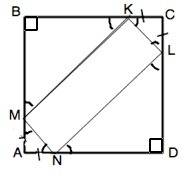
∆ KCL=∆ MAN по двум сторонам и углу между ними. ⇒ MN=KL.
Стороны квадрата равны. Если от равных отрезков отнять по равной части, оставшиеся отрезки будут равны. ⇒
МВ=ВК=LD=ND. -⇒ Прямоугольные ∆ МВК=∆ LDN.
Четырехугольник MNKL – параллелограмм.
Рассмотрим его углы на примере развернутого угла ВМА.
Так как стороны параллелограмма отсекают от углов квадрата равнобедренные прямоугольные треугольники, ∠ВМК=∠NMА=45°. Поэтому ∠КМN=180°-2•45°=90°
Противолежащие углы параллелограмма равны ( можно доказать для каждого угла, что он равен 90°). Тогда сумма двух противолежащих прямых углов равна 180°, и каждый из оставшихся также равен 90°.
Следовательно, четырехугольник КМNL- прямоугольник.
Сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).
Длину неизвестного катета возьмём за х.
12²+х² = 20²
144+х² = 400
х² = 400-144
х² = 256
х = +√256
х = 16
(х = -16 не подходит, так как длина отреза не может выражаться отрицательным числом).
ответ: 16 (ед. измерения).