треугольник АВС, АН=30 и СМ=39 медианы, АМ=МВ, ВН=НС, МН-средняя линия треугольника=1/2АС=26/2=13, АМНС - трапеция, МН параллельна АС, из точки Н проводим линию параллельную СМ до пересечения ее с продолжением АС в точке Е, ЕН=СМ=39, СМНЕ- параллелограмм, СЕ=МН=13, АЕ=АС+СЕ=26+13=39
треугольникАНЕ равнобедренный, АЕ=ЕН=39, проводим высоту ЕТ=медиане=биссектрисе на АН, АТ=ТН=1/2АН=30/2=15, треугольникАТЕ прямоугольный, ЕТ²=АЕ²-АТ²=1521-225=1296, ЕТ=36, площадь АНЕ=площадь трапеции АМНС=1/2*АН*ЕТ=1/2*30*36=540, что составляет 3/4 площади АВС
(площадь треугольника отсекаемого средней линией (МН)=1/4 площади АВС, можно подсчитать самим),
площадь АВС=площадьАМНС*4/3=540*4/3=720
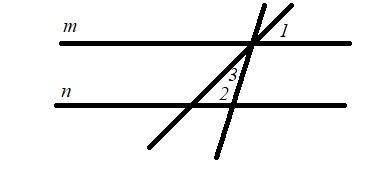
m || n
∠1 = 36˚
∠2 = 104˚
Найти:∠3
Решение:Вертикальные углы равны.
=> ∠1 = ∠4 = 36°, как вертикальные
При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.
∠4 = ∠5 = 36°, как накрест лежащие.
Сумма углов треугольника равна 180°.
∠3 = 180° - (104° + 36°) = 40°
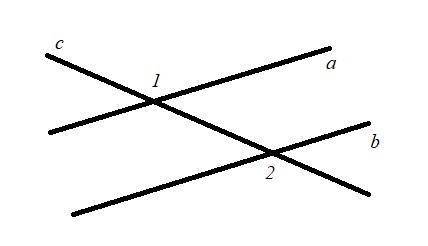
ответ: 40°Задача#2Дано:а || b
∠1 = 124°
Найти:∠2
Решение:Вертикальные углы равны.
=> ∠1 = ∠3 = 124°, как вертикальные.
При пересечении двух параллельных прямых секущей, соответственные углы равны.
=> ∠3 = ∠2 = 124°, как соответственные.
ответ: 124°