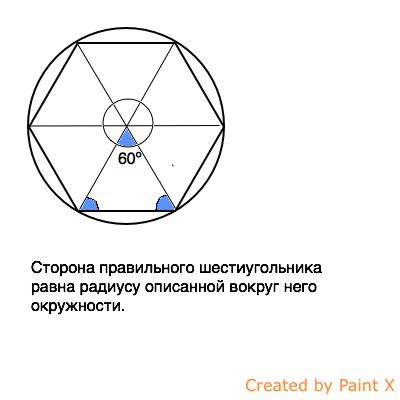
Сторона правильного шестиугольника, вписанного в окружность с радиусом 1, тоже равна 1.
Объяснение:
Так как шестиугольник можно разбить на 6 треугольников, у которых сторонами будут стороны самого шестиугольника и прямые, проведенные от центра шестиугольника к каждому из его углов. Эти маленькие треугольники будут равносторонними. Так как углы при вершине центра шестиугольника будут равны 360°:6=60°. А сам треугольник, считая основанием сторону шестиугольника, будет равнобедренным, так как сторонами будут радиусы описанной окружности. Так как в треугольнике сумма углов 180°, то на эти углы приходится 180°-60°=120°. Так как углы при основании равны, то 120°:2=60° - на каждый из оставшихся углов. Значит каждый из углов равен 60°. Это возможно в равностороннем треугольнике. Значит радиус равен стороне шестиугольника.
ответ: АС=4√7; угол А=40°; угол С=80°
Объяснение: чтобы найти АС воспользуемся теоремой косинусов:
АС²=АВ²+ВС²-АВ×ВС-2×cosB=
=12²+8²-12×8×2×½=144+64-96=112
AC=√112=4√7
По теореме синусов найдём угол А:
sinB/4√7=sinA/8
4√7sinA=8×sinB
4√7×sinA=8×√3/2
4√7×sinA=4√7
sinA=4√3÷4√7
sinA=√3÷√7
Угол А≈40°
Зная что сумма углов треугольника составляет 180°, найдём угол С
Угол С=180-60-40=80°