1) АВ-это отрезок лежит на оси Х, его середина О((4-2)/2;0)=(1;0)
равноудаленные точки от А и В лежат на серединном перпендикуляре к АВ середина О, а прямая, проходящая через нее, перпендикулярно ост х-будет прямая вида x=1
2) Центр окружности О1 (1;y) должен лежать на прямой х=1 и быть на расстоянии 5 от А и В.
тогда AO1=5=√((-2-1)^2+(0-y)^2
5=√(9+y^2)
25=9+y^2
y^2=16
y=+-4
тогда есть 2 окружности радиуса 5 с центрами в O1(1;4) и O2(1;-4)
Тогда уравнения этих окружностей
(x-1)^2+(y-4)^2=25
(x-1)^2+(y+4)^2=25
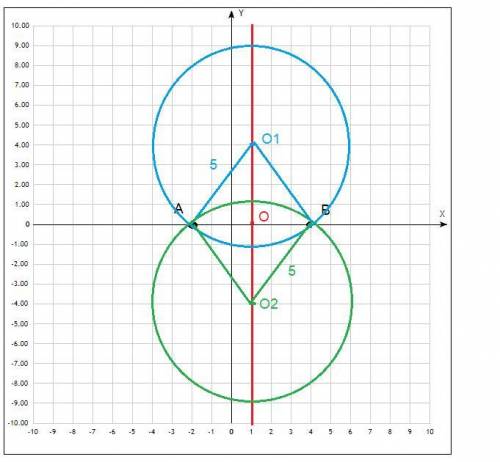
Чертёж смотрите во вложении.
Дано:
ΔАВС.
ВО - биссектриса ∠АВС.
АК - биссектриса ∠ВАС.
Точка М - точка пересечения ВО и АК.
∠АМВ = 177°.
Найти:
∠ВСА = ?
Пусть ∠АВМ = х, тогда и ∠МВК = х (так как ВО - биссектриса ∠АВС) ; ∠ВАМ = ∠МАО = у (так как АК - биссектриса ∠ВАС).
Рассмотрим ΔАМВ. ∠ВМК - внешний, и так как он с ∠АМВ смежный, то ∠ВМК = 180°-177° = 3°. Так как ∠ВМК - внешний, то он равен сумме углов не смежных с ним. То есть, х+y = 3°.
∠АВС = x+x = 2x
∠ВАС = у+у = 2у.
х+у = 3°
2*(х+у) = 2*3°
2х+2у = 6°.
Тогда, по теореме о сумме углов треугольника -
∠ВСА = 180°-(2х+2у)
∠ВСА = 180°-6°
∠ВСА = 174°.
ответ: 174°.