1.)Из точки A проведен к плоскости α перпендикуляр AO = 3 см и две наклонные AB=AC,∠ BAO =∠CAO=60°,∠ CAB=90º. Найдите расстояние между основаниями наклонных.
2.)Сторона равностороннего треугольника равна 6 см. Данная точка находится на расстоянии 2 см от плоскости треугольника и на равном расстоянии от его вершин. Найдите это расстояние и расстояние от этой точки до сторон треугольника.
3.)Гипотенуза равнобедренного прямоугольного треугольника лежит в плоскости, а вершина прямого угла состоит от плоскости на 3 см. Найти угол между плоскостью треугольника и данной плоскостью, если катеты треугольника по 8корень2 см.
(ВСЕ ЗАДАЧИ С РИСУНКАМИ И ЖЕЛАТЕЛЬНО В ПИСЬМЕННОМ ВИДЕ ОТПРАВИТЬ СЮДА ФОТКУ
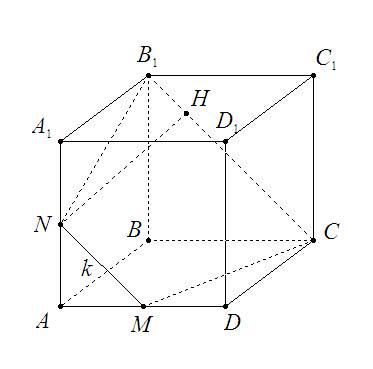
M∈(ABC), C∈(ABC) ⇒ проведем MC
(B1C)∈(BCC1), M∈(ADD1), а т.к. (ADD1) || (BCC1), то секущая плоскость будет пересекать (АDD1) по прямой k, проходящей через точку М параллельно B1C. k пересечет АА1 в точке N, причем AN=NA1.
N∈(AA1B1) и B1∈(AA1B1) ⇒ проведем NB1
MNB1C - сечение куба
2) MN || B1C, CM=B1N=√(a²-(a/2)²)=a√3/2 ⇒ MNB1C трапеция
S (MNB1C) = 1/2 (MN+B1C) * NH, где NH - это высота трапеции
B1C=a√2 / 2
MN = 1/2 B1C = a√2 / 4
B1H = 1/2 (B1C - MN) = a√2 / 4
NH = √(B1N² - B1H²) = a√10 / 4
S (MNB1C) = 3 a² √5 / 16