Объяснение:
1)<AOB=<COD как вертикальные, <C =<A(по усл), BO=OD,
тр АОВ=тр ОСД по гипотенузе и острому углу
2)<A=<C, <AOB=<COD(вертикальные), значит и <B=<D,
3) тр. ABD=тр ACD (AD- общая, АВ=CD) по двум катетам,
значит <B=<C
4) тр АВР= тр А1В1Р1 по гипотенузе( АВ=А1В1 ) и острому углу (<1=<2),
тр АВС= тр А1В1С1 по катету(АВ=А1В1) и прилежащему острому углу
(<1=<2) и следовательно тр АРС=тр А1Р1С1 по катету(АР=А1Р1 и гипотенузеАС=А1С1)
5)тр ВРС= тр АКД по двум катетам (ВК=КД, АК=КС)
Объяснение:
Объём пирамиды:
Значит
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна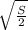
Тогда, по теореме Пифагора: