1)в правильной четырехугольной пирамиле все боковые грани — правильные треугольники. найдите косинус угла между апофемами смежных боковых граней пирамиды, если длина бокового ребра равна 4.1)1/3 2)2/33)3/44)3/52)высота правильной треугольной призмы abca1b1c1 равна 2корень7, а сторона основания равна 3. найдите площадь сечения, проходящего через вершину а и середины ре-бер bв1 и сс1.1) 113) 1,5/552) 3/554) 13ришите мне с даном и решением нужно 20

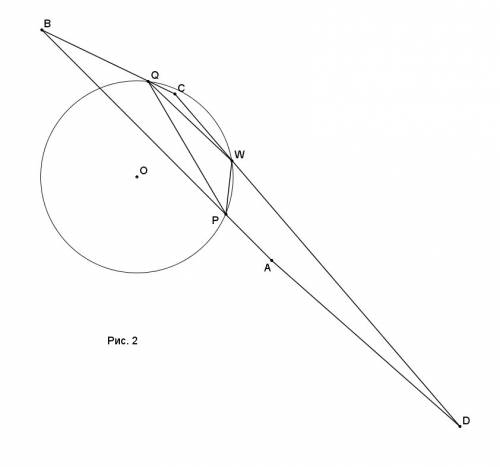
20²·sin²∠Q=16²+12²-2·16·12·cos∠Q. Решаем это уравнение, получаем cos∠Q=0 и cos∠Q=24/25. Т.е. в первом случае PQW - действительно прямоугольный (см. рис. 1), а второй случай также существует при выпуклом ABCD (см. рис. 2.)
Т.к. AB/PB=CB/QB=5/4, то треугольник ABC подобен треугольнику PBQ с коэффициентом подобия 5/4, откуда AC=(5/4)·PQ=5*16/4=20 и AC||PQ. Аналогично, треугольник BCD подобен треугольнику QCW с коэффициентом 5, т.е. BD=5QW=5*12=60 и BD||QW, откуда угол между диагоналями ABCD равен углу PQW. Поэтому, площадь ABCD вычисляется по формуле (1/2)AC·BD·sin(∠PQW).
Значит, в случае, когда PQW - прямоугольный
S(ABCD)=(1/2)·20·60·sin(90°)=600.
Во втором случае
S(ABCD)=(1/2)·20·60·√(1-24²/25²)=168.