Любая линейная функция выражается формулой y = kx + b. Подставим известные нам значения x и y из точек в эту формулу и составим систему:
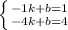
Вычтем из второго уравнения первое и найдём k:
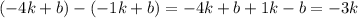
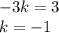
Подставим найденный k в любое уравнение линейной функции из системы, чтобы найти b:
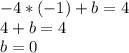
Таким образом, уравнение первой линейной функции f (x) выглядит как y = -1x + 0, или, упрощая, y = - x.
Повторим те же действия с точками функции g (x). Составляем систему:
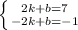
На этот раз проще будет сначала найти b, так как это можно сделать сложением двух уравнений:
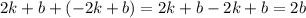
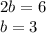
Подставляем в уравнение из системы:
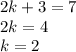
Таким образом, уравнение второй линейной функции g (x) выглядит как y = 2x + 3.
Чтобы найти точку пересечения графиков линейных функций, необходимо приравнять их формулы друг к другу, чтобы найти общую абсциссу. Получаем:
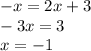
Найдём значение ординаты y в точке пересечения по любой из формул:
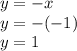
Таким образом, графики функций f (x) и g (x) пересекаются в точке (- 1; 1).
В основе прямой призмы лежит равнобедренная трапеция с основаниями 4см и 10 см и боковой стороной 5 см. Боковое ребро призмы равно 10 см. Вычислите полную поверхность призмы.
Объяснение:
В прямой призме боковое ребро перпендикулярно площади основания.
S( полной)=S(боковой)+2S(основания);
S(боковой)=Р(основания)*h, где h-ребро боковое призмы;
S(основания)=S(трапеции)=1/2*(а+в)*h ,где h-высота трапеции
S(боковой)=(4+10+2*5)*10=240 (см²).
АВСД-равнобедренная трапеция АВ=СД=5 см ; пусть ВН⊥АД, СК⊥АД ⇒ АН=(10-4):2=3 (см)
ΔАВН-прямоугольный , по т. Пифагора ВН=√(5²-3²)=4 (см).
S(трапеции)=1/2*(4+10)*4=28(см²)
S( полной)=240+2*28=296(см²)