SR - апофема пирамиды. Площадь боковой поверхности состоит из суммы площадей 3-х равных треугольников, которые являются боковыми гранями пирамиды. То есть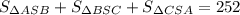 
. В данном случае речь идет о треугольнике BSC. так как площади треугольников равны, то можно записать в следующем виде 
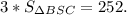Делим обе части на 3. 
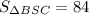. Так как треугольник BSR - равнобедренный (из того, что пирамида -правильная), то его площадь равна произведению половины основания BC на высоту SR. Так как пирамида правильная, то AB=BC.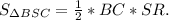 
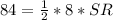. Делим обе части уравнения на 4. 
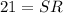, то есть SR=21.
Найдем сначала угол при основании этого треугольника. Так как у равнобедренного треугольника углы при основании равны, то можно, обозначив угол при основании через альфа и имея ввиду, что сумма углов треугольника равна 180 градусам, составить уравнение.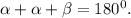 
То есть 
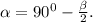. Если рассмотреть треугольник, образованный высотой h, основанием исходного треугольника и частью боковой стороны, то можно увидеть, что основание треугольника является его гипотенузой. h - противолежащая сторона к углу при основании треугольника, который мы вычислили. Значит гипотенузу можно найти как отношение катета h к синусу угла при основании большого треугольника. ответом будет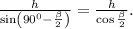 
Высота призмы равна 10 (высота, ребро призмы и проекция ребра на основание образуют равнобедренный прямоугольный треугольник с гипотенузой 10*корень(2)).
Осталось вычислить площадь основания, то есть найти площадь треугольника со сторонами 4, 13 и 15.
Это, конечно же, можно сделать по формуле Герона. Так сказать - тупой Надо только не забывать,что в формуле Герона р - ПОЛУпериметр, то есть для этого треугольника
р = 16, p - a = 12, p - b = 3, p - c = 1,
S^2 = 16*12*3*1 = 16*36,
S = 24.
Отсюда Объем призмы V = 240 куб.см.
Однако, площадь можно вычислить и гораздо проще, если кое о чем удачно догадаться. Если провести высоту из вершины, общей для сторон 13 и 15 на продолжение стороны 4, то МОЖНО увидеть 2 египетских треугольника, один со сторонами 9, 12, 15 и другой - со сторонами 5, 12, 13. Заданный треугольник является "разностью" этих треугольников (9 - 5 = 4, а 12 - общая высота).
Отсюда S = 4*12/2 = 24.