Площадь ромба равна 120 см², а одна из диагоналей больше другой на 14 см. Найдите длину неизвестной диагонали.
▔ ▔ ▔
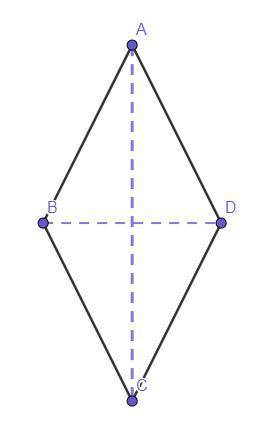
★☆★ Чертёж смотрите во вложении ★☆★
Дано:Четырёхугольник ABCD — ромб.
S(ABCD) = 120 см².
AC и BD — диагонали.
АС = BD+14 см.
Найти:BD = ?
Решение:Пусть BD = х.
Тогда —
АС = х+14 см.
▸Площадь ромба равна половине произведения его диагоналей◂
То есть —
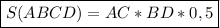
Подставим в формулу известные нам значения —
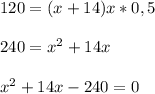
Решаем полученное квадратное уравнение —
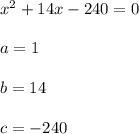
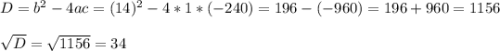
Ищем корни —
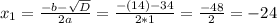
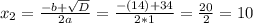
Как видим, корень х₁ не подходит, так как длина отрезка не может выражаться отрицательным числом.
Поэтому, BD = х = 10 см.
ответ:10 см.
Конус.
L = 10 см
S осн = 36п см²
Найти:V - ?
Решение:S осн = S круга = пR² = 36п см² => R = √36 = 6 см
Осевое сечение данного конуса - (если ось плоскость проходит через ось конуса) - равнобедренный треугольник, а высота h делит этот равнобедренный треугольник на два равных прямоугольных треугольника (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что у нас треугольник - равнобедренный).
Найдём высоту h, по теореме Пифагора: (c = √(a² + b²), где с - гипотенуза; a, b - катеты)
h = √(L² - R²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
Итак, h = 8 см.
V = 1/3пR²h = п(1/3 * 6² * 8) = 96п см³
ответ: 96п см³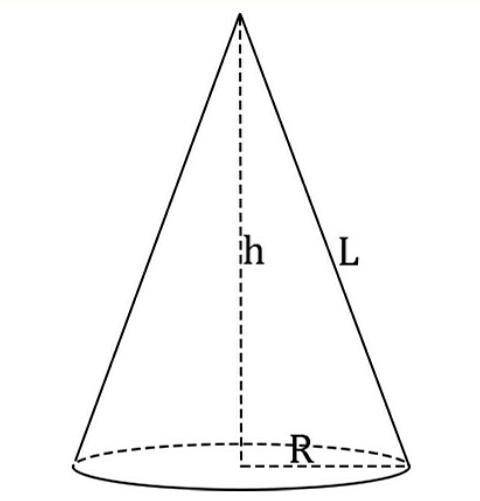
Відповідь: - 6
Пояснення: фото