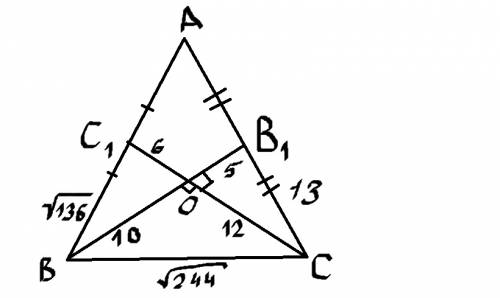
Задача решается проще, если вспомнить, что медианы в точке пересечения (т. е. все три медианы в любом треугольнике пересекаются внутри него строго в одной точке - это центр тяжести треугольника). Так вот эти медианы делятся в точке пересечения в соотношении 2 к 1, считая от вершины. Значит ВО=15*2/3=30/3=10 см, СО=18*2/3=6*2=12 см.
ОВ1=15/3=5 см, ОС1=18/3=6 см. Теперь нужно вспомнить теорему Пифагора. Треугольник ВОС - прямоугольный, значит ВС - гипотенуза.
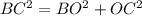
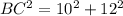
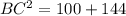
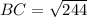
Треугольник ВОС1 - тоже прямоугольный, так как угол С1OB - прямой. Доказывается так.
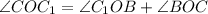
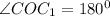 - как развернутый угол.
- как развернутый угол.
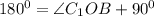
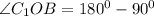
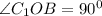
По теореме Пифагора из треугольника находим гипотенузу ВС1.
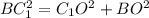
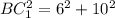
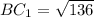
Заметим, что BC1 - половина АВ по определению медианы СС1.
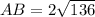
Треугольник B1OC - прямоугольный, так как угол B1OC - прямой, как вертикальный к углу С1OB. Та же теорема Пифагора, чтобы вычислить гипотенузу В1С.
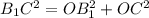
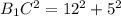
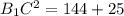
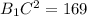
B1C=13 см.
Заметим также, что В1С - половина АС. Значит АС=26 см.
Вычислим периметр АВ.
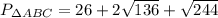
построем рисунок, в треугольнике ВСD: ВС=СD (т.к. шестиугольник правильный), угол равен 120 градусов, (по формуле для нахлждения угла в правильном многоугольнике а=180(n-2)/n), проведһм перпендикуляр СН, угол ВHC = (180-120)/2=30 (т.к. треугольник равнобедренный, углы при основании равны) следовательно, СН=0,5ВС = корень из 48 по полам=корень из двенадцати (после преобразования)
теперь ВН = (по теореме пифагора) корень из (48-12) = корень из 36 = 6
ВН равно HD (т.к. в равнобедренном треугольнике высота равна медиане) следовательно ВD=2BH = 6*2 = 12
Как то так!
полупериметр равен 11, синус 60° равен √3/2, площадь параллелограмма равна произведению его смежных сторон на синус угла между ними, если одна из сторон равна х см
, то другая, смежная ей, равна 11-х, а площадь
х*(11-х)*√3/2=14
х²-11х+28/√3=0
х=(11±√(121-112/√3))/2,
х=(11±√(121-112/√3))/2≈(11±55)/2; подходит только положительный корень, второй , отрицат., не подходит
х=33, значит, одна сторона да и первый не подходит. т.к. получаем, что сторона больше периметра. чего быть не может.
Задача составлена некорректно