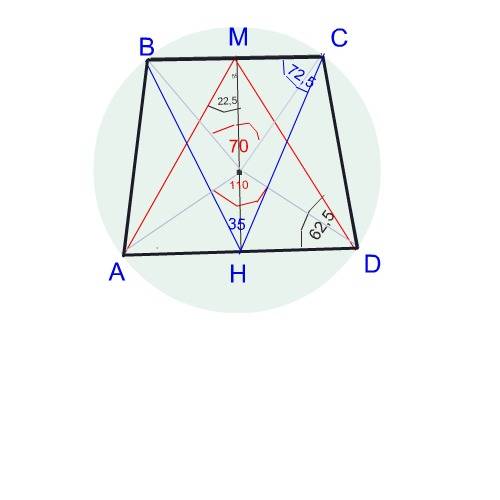
Рисуем трапецию в окружности.
Дополним рисунок треугольниками АМD и ВНС.
Углы при вершинах этих треугольников равны половине центральных углов ( под которыми видны из центра окружности основания трапеции)
Путем несложных вычислений находим углы треугольников DМН и МНС
Для решения применена теорема синусов.
Синусы найденных углов
72,5=0,9537
62,5=0,8870
22,5=0,3826
17,5=0.3007
---------------------------------
МН:sin 62,5=8:0,887=9,019
DН=9,019∙ sin22,5=3,4507
AD=6,9
-------
МН:sin 72,5=8:0,9537=8,3884
СМ=8,3884∙sin17,5=2,52
ВС=5,04
Ясно, что значения длин сторон округленные.
-------------
Площадь трапеции равна произведению полусуммы оснований на ее высоту.
S ABCD=8(6,9+5,04):2=95,52 (?)³
2) Углы, которые образовываются при пересечении двух прямых - смежные, их сумма равна 180. Обозначив меньший угол за x получим уравнение:4x+x=1805x=180x=36Это меньший угол. А больший равен 36*4=144
3) Если с- биссектриса угла ав, то угол ас=углу св. Но d делит угол ас пополам. Каждая половина равна 20 градусов, значит весь угол ас равен 40. Но ас=св, поэтому имеем, угол bd = 20+40=60 градусов.
4)Если с- биссектриса угла ав, то угол ас=углу св. Но d делит угол ас пополам. Каждая половина равна 20 градусов, значит весь угол ас равен 40. Но ас=св, поэтому имеем, угол bd = 20+40=60 градусов.