
Площадь боковой поверхности треугольной призмы состоит из суммы площадей трех ее граней, которые являются прямоугольниками. Площадь одной грани будет равна 72/3=-24 см. В призме высота равна ребру, т.е. одной из сторон прямоугольной грани и равна 6 см. по условию задачи. Найдем длину стороны основания, которая является и стороной грани призмы из формулы площади прямоугольника ах6=24, т.е. сторона а = 4. Т.к. в основании правильной треугольной призмы лежит равнобедренный треугольник (все его стороны и углы равны), то можем вычислить его площадь
S= 1/2х4х4хsin60=8√3/2=4√3
Объяснение:
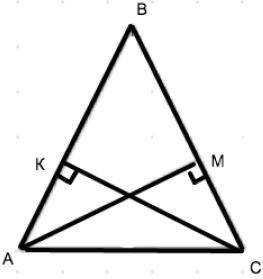
1. Из треугольника АСК и АМС:
АС-общая сторона
угол К=углу М=90°
АМ=СК по условию
(дальше ставим палочку по всему решению и знак следствия)
=> треугольник АСК= треугольник АМС по 2 сторонам и углу между ними.
2. треугольник АСК=треугольник АМС, значит угол ВАС=ВСА.
Угол ВАС=ВСА, значит треугольник АВС равнобедренный по обратному свойству о равнобедненном треугольнике: если углы при основании равны, то треугольник равнобедренный.