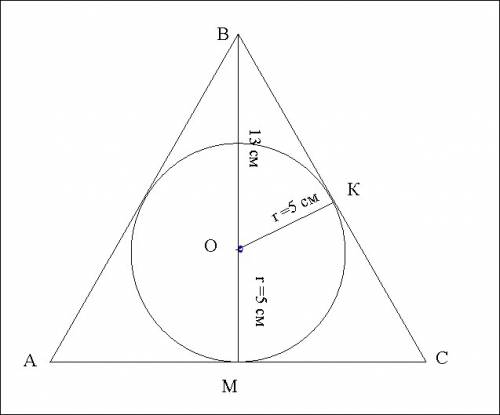
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см
Объяснение:отвечаю без чертежа
1)перпендикуляр,проведенный с вершины прямого угла к гипотенузе
является средним пропорциональным между отрезками,на которые он делит гипотенузу(т.е. 9 и 4 ),зто записывается так h²=4·9=36, h=6
2)а теперь по т.Пифагора находишь катеты:
а) а²=9²+6²=81+36=117, а=√117=3√13;
б)в²=4²+6²=16+36=52, в=√52 =2√13
можно и по другому: каждый катет явл. средним прпорциональным между гипотенузой и отрезком его на гипотенузу:а²=13·9⇒а=3√13
в²=4·13⇒в=2√13.