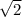Объяснение:
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.
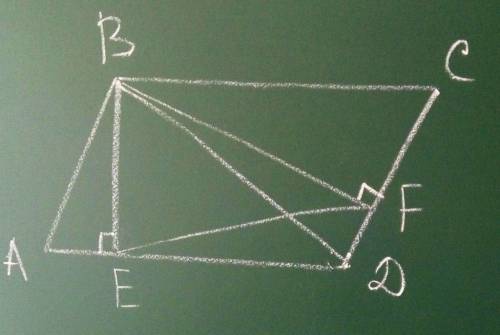
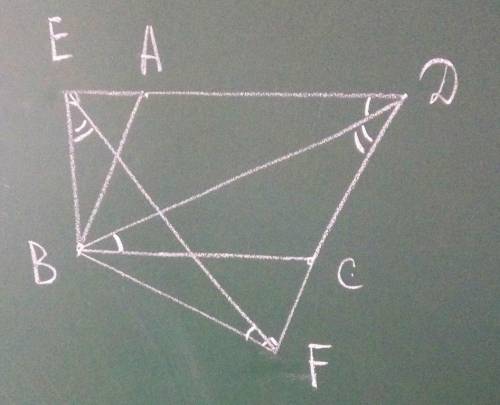
24 см
Объяснение:
Дано: ΔАВС - прямокутний, ∠А=90°, ВС-АВ=4 см, АС=12 см. ВМ=АМ=СМ=26 см. МН⊥АВС. МН - ?
Якщо точка М віддалена на однакову відстань від усіх вершин ΔАВС, значить, точка Н знаходиться у центрі описаного кола. Центр описаного кола у прямокутного трикутника знаходиться посередині гіпотенузи.
Знайдемо гіпотенузу ВС за теоремою Піфагора:
ВС=х см, АВ=х-4 см
х²=(х-4)²+АС²
х²=х²-8х+16+144
8х=160; х=20
ВС=20 см.
ВН=СН=АН=20:2=10 см (це радіуси описаного кола)
Розглянемо ΔАМН - прямокутний.
МН=√(АМ²-АН²)=√(676-100)=√576=24 см
ответ: S = 30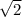
Объяснение:
Площадь параллелограмма равна произведению смежных сторон на синус угла между ними
S=a*b*sin45° = 12*5*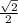 =30
=30