ответ: 6 (ед. длины)
Объяснение:
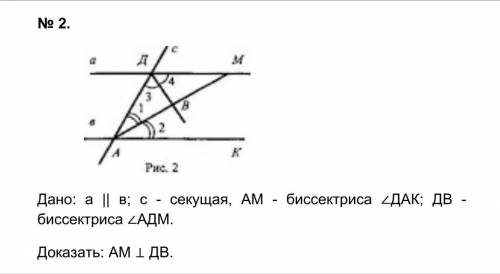
Проведем DE║AM. В треугольнике АМС отрезки АD=DC ( т.к. ВD медиана ∆ АВС и делит АС пополам). DE параллельна АМ и является средней линией ∆ АМС.⇒ СЕ=ЕМ.
В ∆ ВDE отрезок ОМ - средняя линия ( ВО=ОD, и ОМ║DE). ⇒ ВМ=МЕ=ЕС.
Аналогично, проведя из D параллельно СК прямую DH доказывается равенство ВК=КН=НА. ⇒ Так как ∆ АВС равнобедренный, ВК=ВМ. Треугольник КВМ подобен ∆ АВС по пропорциональным сторонам и углу между ними. Коэффициент подобия k=ВМ:ВС=1/3, откуда КМ=АС:3=18:3=6 (ед. длины).

ИЛИ по теореме Менелая для ΔВСD и секущей АМ ⇒ CM/MB • BO/OD • AD/AC = 1 ; CM/MB • 1 • (9/18) = 1 ⇒ CM/MB = 2
Аналогично для ΔABD и секущей КС ⇒ AK/KB = 2
Значит, BK/KA = BM/MC = 1/2 ⇒ ΔКВМ подобен ΔАВС по двум пропорциональным сторонам и равному углу между ними: МК || АСВК/АВ = ВМ/ВСМ= МК/АС ; ВМ/ВС = МК/АС1/3 = КМ/18 ⇒ КМ = 18/3 = 6 ОТВЕТ: 6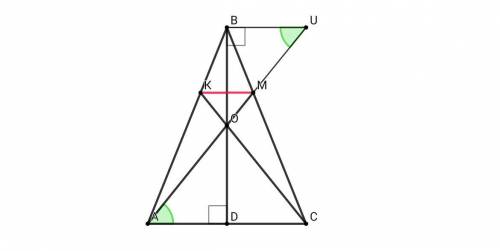
а || b
c - секущая.
АМ - биссектриса ∠DAK
DB - биссектриса ∠ADM
Доказать:АМ ⊥ DB
Решение:При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 180°.
Возьмём любые градусные меры углов DAK и ADM, но при условии, что их сумма будет равна 180°.
Допустим ∠DAK = 100˚, тогда ∠ADM = 80˚
Так как АМ и DB - биссектрисы => ∠1 = ∠2 = 100°/2 = 50° и ∠3 = ∠4 = 80°/2 = 40°
В прямоугольном треугольнике сумма острых углов равна 90°
40° + 50° = 90° => △ADB - прямоугольный.
=> DB ⊥ AM
Вывод: мы можем взять любые градусные меры ∠DAK и ∠ADM, но при условии, что сумма их будет равна 180°.
Ч.Т.Д.