Чтобы найти объем прямоугольного параллелепипеда нужно перемножить его высоту, ширину и длину. То есть
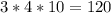
ОТВЕТ №1: Объем прямоугольного параллелепипеда равен 120 см²
Чтобы найти площадь основания конуса, нужно найти радиус. Если образующая наклонена под углом в 60°, то высота конуса равна половине ее длине (по свойству прямоугольного треугольника).
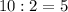
Чтобы найти радиус нужно воспользоваться теоремой Пифагора
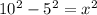
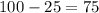
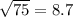 (примерно)
(примерно)
Теперь мы распологаем всеми значениями для вычисления объема
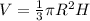
Подставляем значения
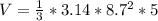

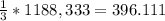
ОТВЕТ №2: Объем конуса равен примерно 396.111 см²
<ABE=<CBE.
Рассмотрим треугольники МРВ и МКВ. Они равны по стороне и двум прилежащим к ней углам:
- ВМ - общая сторона;
- <ABE=<CBE, как показано выше;
- <BMP=<BMK по условию.
У равных треугольников равны соответственные стороны ВР и ВК. Тогда треугольник РВК - равнобедренный, где ВМ - биссектриса, проведенная к его основанию РК (поскольку <ABE=<CBE). В равнобедренном треугольнике биссектриса, проведенная к основанию, является также и высотой. Значит ВМ перпендикулярна основанию РК.