ответ:1056+1584√3 (см²)
Объяснение: 1)Пусть параллелограмм АВСД-нижнее основание призмы,А₁В₁С₁Д₁-верхнее основание; ∠А=30°, тогда ∠Д=180°-30°=150°. 2)Боковая поверхность призмы S= P·h, P= 2·(АД+СД)= 2( 16+24√3)=32+48√3. 3)Вычислим большую диагональ основания АС по теореме косинусов из ΔАДС: АС²= АД²+СД²- 2·АС·СД·CosД= 16²+(24√3)² - 2·16·24√3·Cos150°= 256+1728 - 2·16·24√3· (-Cos30°)=256+1728 + 2·16·24√3· √3/2 =256+1728 +1152=3136, ⇒АС = √3136= 56. 4)Рассмотрим прямоугольный треугольник АА₁С, по условию большая диагональ призмы А₁С=65 см.⇒h²= AA₁²= А₁С²- AC²65²-56²= 1089, h=√1089=33 (cм) 5) Боковая поверхность призмы S= P·h =(32+48√3) P= 2·(АД+СД)= 2( 16+24√3)=(32+48√3)· 33 =1056+1584√3 (см²)
28 см
Объяснение:
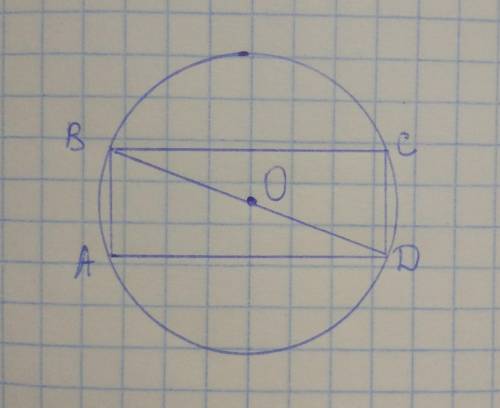
Дано: ABCD - прямоугольник, AD=(АВ+2) см, ω(О; ОА) - описанная, R=5 см
Найти Р
Решение
1) Диагонали АС и BD прямоугольника пересекаются в т. О => OA=OB=OC=OD=R, тогда BD=2R=2OA=5×2=10 см
2) Пусть АВ=х см, x>0, тогда AD=(х+2) см
∆ABD, <BAD=90°, по теореме Пифагора BD²=AB²+AD²
10²=x²+(x+2)²
100=x²+x²+4x+4
2x²+4x-96=0
x²+2x-48=0
По теореме Виета для приведенного квадратного уравнения
{ х1+х2= -b= -2
{ x1x2= c= -48
x1= -8 - посторонний корень, x2= 6 см= AB
AD= x+2= 6+2= 8 см
3) Р= 2(AB+AD)= 2×(6+8)=14×2= 28 см
Розв'язок:
Опустимо висоту CH з вершини C на сторону AB.
Тоді відрізок AH = x cm, а відрізок BH = √13−x cm.
Виразимо висоту CH з прямокутних трикутників ACH та BCH за т. Піфагора:
Зрівняємо праві частини рівнянь:
Підставимо значення та знайдемо невідому змінну:
Тобто, AH = x = 4/√13 cm.
Знайдемо довжину висоти CH за т. Піфагора з ΔACH:
Підставимо значення у формулу площі трикутника:
Відповідь: Площа трикутника ABC рівна 3.5 cm².