1. Рассмотрим треугольники, образованные соединением середин сторон треугольника. Они равны (по прямым углам и катетам). Значит гипотезы равны => у четырёхугольника все стороны равны. 2. Рассмотрим противолежащие углы образованного четырёхугольника. Они равны развёрнутому углу минус два равных угла, прилежащих к гипотенузе. Так как треугольники равны, то соответствующие углы равны, значит и противолежащие углы четырёхугольника равны. 3. Параллелограмм, у которого все стороны равны, является ромбом. Четырёхугольник, у которого противолежащие углы равны, является параллелограммом. Следовательно, четырёхугольник - ромб. Ч.т.д.
Проведем диагональ трапеции и рассмотрим образовавшиеся треугольники. Пара противоположных сторон ромба являются средними линиями этих треугольников, каждая из них параллельна этой диагонали и равна ее половине. Отсюда эта пара - равные и параллельные стороны, т.е. четырехугольник - параллелограмм. Аналогично другая пара противоположных сторон равны. А т.к.к трапеция равнобедренная, то ее диагонали равны. Значит все стороны четырехугольника равны. Таким образом, четырехугольник - параллелограмм с равными сторонами, т.е. ромб.
Площадь поверхности шара равна
S=1764π квадратных единиц.
Объяснение:
По формуле объема шара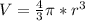 . Подставим известные данные.
. Подставим известные данные.
Разделим обе части на π.
Делим обе части на 4. Получаем
Обе части умножим на 3. Получим
3*3087=r³.
3*3²*343=r³.
3³*7³=r³.
Извлечем кубический корень из обеих частей. Получим
r=3*7
r=21 единицы.
Площадь поверхности шара равна первой производной от объема шара S=4πr² квадратных единиц.
S=4π*21²
S=4*441π
S=1764π квадратных единиц.