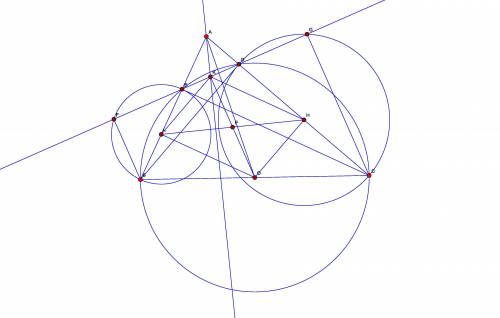
См. чертеж.
Построенные окружности "демонстрируют" скрытые связи, которые есть в конструкции. Если их мысленно убрать, получится построение из условия задачи.
Так как EC перпендикулярно AB, точка Е лежит на окружности. построенной на BC, как на диаметре, и центром этой окружности будет середина BC - точка O. Точно также - точка D. Аналогично, L - середина BE, H - середина CD.
Первое. Я собираюсь доказать, что FE = DG; но делать я это буду "через Китай". Пусть точка K - середина ED. Если удастся доказать, что K лежит на радикальной оси окружностей (BFE) и (DGC), то из этого автоматически будет следовать FE = DG
Про радикальную ось этих окружностей известно две вещи. Во-первых, она перпендикулярна линии центров LH; во-вторых, она проходит через точку A, поскольку точка A - радикальный центр всех трех окружностей, изображенных на чертеже. В самом деле, AB и AC - радикальные оси пар окружностей (BFE) (BCED) и (DGC) (BCDE), а значит, их общая точка имеет равные степени относительно (BFE) и (DGC) (я повторил доказательство теоремы о радикальном центре).
Таким образом, задача свелась к тому, что надо доказать перпендикулярность AK и LH.
Треугольники ADE и ABC подобны, => AO и AK - соответствующие медианы в подобных треугольниках (я пока не знаю, понадобится ли это для решения).
Четырехугольник KHOL - параллелограмм Вариньона для четырехугольника BEDC; его стороны параллельны BD и CE и равны их половинам. => ∠KHO = ∠BAC; (стороны этих углов взаимно перпендикулярны) кроме того, KH = CE/2 = AC*sin(A)/2; HO = BD/2 = AB*sin(A)/2; то есть треугольники ABC и KHO подобны с коэффициентом sin(A)/2; => треугольник KHO подобен треугольнику EAD, Стороны их одинаково ориентированы (см чертеж, например, ясно, что при повороте на "минус" 90°, то есть по часовой стрелке, и каком-то сдвиге и сжатии, соответствующие стороны переходят друг в друга, EA -> KH; AD -> HO;) => существует поворотная гомотетия, переводящая EAD -> KHO, при этом угол поворота равен 90°, поскольку стороны взаимно перпендикулярны. Ясно, что при этом AK -> HP (Р - точка пересечения диагоналей параллелограмма KHOL, и => середина KO и HL); поэтому AK перпендикулярно HP чтд.
Итак, K лежит на радикальной оси окружностей (BFE) и (DGC), и поскольку KE = KD, EF = DG; (в переводе на "человеческий" язык это означает вот что - у точки K - середины DE, - равны степени относительно этих окружностей, то есть KG*KD = KF*KE; поскольку KE = KD, KF = KG; => EF = DG;)
по условию FG = 7; DE = 3; => EF = DG = 2;
Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров. Для остроугольного треугольника этот центр будет в треугольнике. Построение. Построить нужный треугольник не составляет труда. 1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. . Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности. Расстояние от него до вершин треугольника равны радиусу описанной окружности. 2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника. 3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны. Как это выглядит, дано в приложени
а=12 см
Объяснение:
Pосн=4а, а - сторона основания правильной пирамиды
2а=24, а=12