ответ: 3x + 4y - 3z - 2 = 0.
Объяснение:
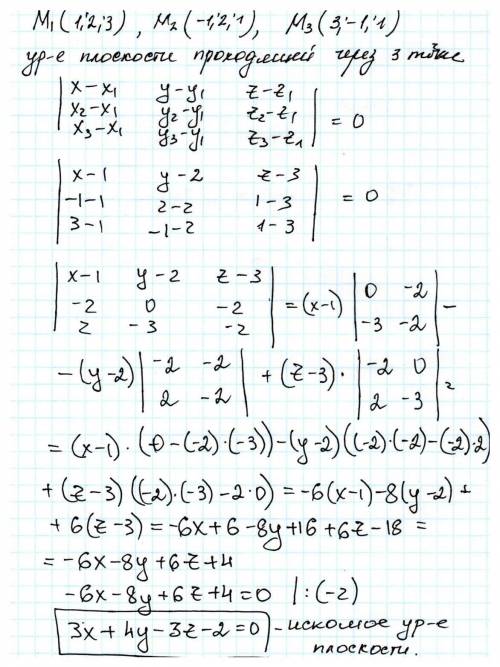(1; 2; 3),м [tex]м_{2}[/t" />
Мое личное отношение к Базарову двойственно. С одной стороны, он мне нравится: он умен, образован, честен, обладает большой силой воли. Все эти качества в человеке привлекают. Но, с другой стороны, я считаю, что надо сначала построить что-то новое, а потом ломать старое, а не наоборот. Иначе может получиться так: сломав все, что было, мы не сумеем создать что-то новое. Также мне кажется нелепым отрицать все: природу, искусство, музыку, любовь, даже то, чего не знаешь. Как можно отрицать то, чего не знаешь? Этого я не понимаю.
Мне жаль Базарова, который в конце романа умирает. Вместе с ним умирают и те идеи, о которых он говорил. И все же… Поместив в центр романа споры Базарова и Кирсанова, Тургенев недвусмысленно дал понять, кому из них принадлежит будущее. Базаров, по мысли автора, человек несовершенный, но «живой», а не «застывший», как Павел Петрович. Пусть главный герой романа пока одинок, он — предвестник будущих перемен.
Объяснение:
спиши
Решим задачу так:
1. Построим прямую а и точку А на ней.
2. Из точки А построим угол, равный известному нам, и под этим углом прямую b
3. Построим прямую д, паралелльную b, на расстоянии, равном высоте h из условий задачи. Обозначим точку В пересечения прямых b и д.
4. Из точки В построим известный нам угол "в другую сторону" (т.е. не параллельно прямой b) и прямую с под этим углом. Обозначим точку С пересечения прямых
б и с.
Ура, треугольник АВС построен.
Для доказательства построим из точки В отрезок ВЕ перпендикулярный отрезку АС. Поскольку точка В лежит на прямой д, параллельной отрезку АС и находится на расстоянии h, значит ВЕ является высотой, построенной к боковой стороне и равно h
Пусть (х1, х2, х3), (у1, у2, у3) и (z1, z2, z3) – координаты первой, второй и третьей точки соответственно. Тогда уравнение плоскости, проходящей через эти точки определяется из выражения:
(x-x1)*(у2-y1)*(z3-z1) – (x-x1)*(z2-z1)*(y3-y1) – (y-y1)*(x2-x1)*(z3-z1) + (y-y1)*(z2-z1)*(x3-x1) + (z-z1)*(x2-x1)*(y3-y1) – (z-z1)*(y2-y1)*(x3-x1) = 0.
Подставив координаты точек в это выражение, получаем уравнение плоскости через точки М₁М₂М₃: 3x +4y - 3z - 2 = 0.
Это же уравнение можно получить через определитель:
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x - 1 y - 2 z - 3
(-1) - 1 2 - 2 1 - 3
3 - 1 (-1) - 2 1 - 3 = 0
x - 1 y - 2 z - 3
-2 0 -2
2 -3 -2 = 0
(x - 1) 0·(-2)-(-2)·(-3) - (y - 2) (-2)·(-2)-(-2)·2 + (z - 3) (-2)·(-3)-0·2 = 0
(-6) x - 1 + (-8) y - 2 + 6 z - 3 = 0
- 6x - 8y + 6z + 4 = 0
3x + 4y - 3z - 2 = 0.