Что бы доказать, что площадь прямоугольника ABCД равна площади треугольника AEД, надо доказать, что площадь треугольника ЕВО=площади треугольникаОСД (т.е. треугольники равны), т.к. пдощадь АВСД=площадьАВОД+площадьОСД.
АВ=ВЕ (по построению)
АВ=СД (по св-вам прямоугольника)
следовательно ВЕ=СД
уголОЕВ=углуСДО (т.к. накрест лежащие для АЕ II СД и секущей ЕД)
угол ОСД=углуЕВО=90градусов
следовательно тр.ВЕО=тр.ОСД по стороне и двум прилежащим углам (по II признаку)
Если аб основание, тогда св боковая сторона, поскольку трапеция р/б, то св = ад = 10см, Проведём высоты из вершины тупых углов к большему основанию, обазначим их, как СМ и ДН. Получили два прямоугольных треугольника, которые равны по трём углам. Поскольку в р/б трапеции углы при основании равны, значит угол БСМ = углу АДН = 30градусам. АН и БМ из равенства треугольников равны. Также они лежат напротив угла в 30 градусов, соответсвенно равны 1/2 гипотенузы Т.е СВ, значит они равны 5 см. У нас остаётся отрезок МН = СД по свойству р/б трапеции. Поскоьку АБ=16, а АН и БМ 5 см, то НМ = СД = 6 см ответ: СД = 6 см
№1
S1=8*8=64
S2=15*15=225
S3=225+64=289
сторона третьего квадрата =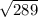 = 17см.
= 17см.
№2.
Е
В О С
А Д
Что бы доказать, что площадь прямоугольника ABCД равна площади треугольника AEД, надо доказать, что площадь треугольника ЕВО=площади треугольникаОСД (т.е. треугольники равны), т.к. пдощадь АВСД=площадьАВОД+площадьОСД.
АВ=ВЕ (по построению)
АВ=СД (по св-вам прямоугольника)
следовательно ВЕ=СД
уголОЕВ=углуСДО (т.к. накрест лежащие для АЕ II СД и секущей ЕД)
угол ОСД=углуЕВО=90градусов
следовательно тр.ВЕО=тр.ОСД по стороне и двум прилежащим углам (по II признаку)
Что и требовалось доказать.