Установіть відповідність між геометричною фігурою (1–4) та її площею (А – Д)
1 ромб зі стороною 6 см і тупим кутом 120 0
2 квадрат, у який вписане коло радіуса 2 см
3 паралелограм, одна сторона якого дорівнює 5 см,
а висота, проведена з вершини тупого кута,
ділить іншу сторону на відрізки 4 см і 2 см
4 прямокутник, більша сторона якого дорівнює 6 см й
утворює з діагоналлю кут 30
А
Б
В
Г
Д
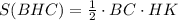, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
.
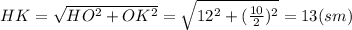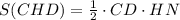, где НN - высота, проведенная к стороне СD.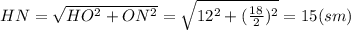
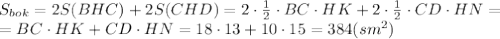
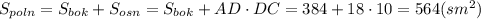
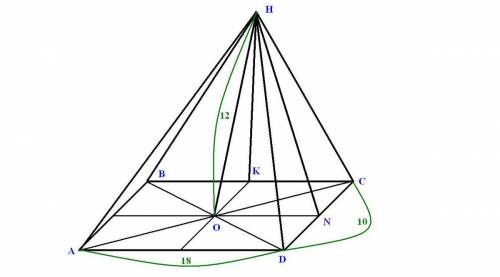
Найдите площадь полной поверхности прямой призмы, в основании которой лежит ромб со стороной a=8 см и острым углом 60°, если большая диагональ призмы наклонена к плоскости ее основания под углом 30°.
Дано : ABCDA₁B₁C₁D₁ прямая призма ( AA₁ ⊥ пл.ABCD )
AB=BC=CD=DA = a = 8 см ( ABCD - ромб)
∠BAD = 60°
∠B₁CA = 30 ° - - - - - - -
Sполн пов - ?
Sполн пов= 2Sосн + Sбок = 2*a*a*sin60° +4a*h || h =AA₁ ||
Sполн пов= a²√3 + 4a*h
Из ΔA₁AC : AA₁ =AC*tg(∠B₁CA) =AC*tg30° = AC/√3 =a√3 /√3 = a
Δ ABD - равносторонний (∠BAD = 60°) ⇒ AO =a√3 /2 ; AC=2AO =a√3
Sполн пов= a²√3 + 4a² =a²(4+√3) =8²(4+√3) см²= 64(4 +√3) см²
ответ: 64(4 +√3) см² || (256+64√3) см² ||
подробности см приложение