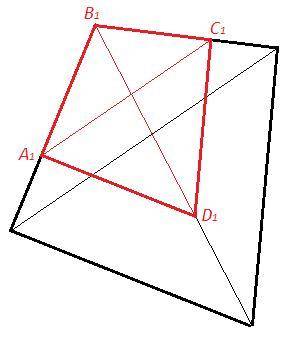
Соответствующие диагонали разбивают подобные многоугольники на подобные треугольники.
Доказываем подобие треугольников (с одинаковым коэффициентом и соответствием сторон) - тем самым доказываем подобие многоугольников.
(3) A1B1C1~ABC, A1D1C1~ADC (по двум сторонам и углу между ними)
(4) A1B1C1~ABC (по данным смежным сторонам и углу между ними)
A1D1C1~ADC (по стороне (A1C1, AC) и прилежащим углам)
(6) A1B1C1~ABC, A1B1D1~ABD (по трем пропорциональным сторонам)
∠C1A1D1=∠CAD
C1A1D1~CAD (по двум сторонам и углу между ними)
Угол АОС =150°. Смежные с ним углы АОД и СОЕ равны 180° - 150° = 30°. Медианы треугольника точкой пересечения О делятся в отношении
2:1, начиная от вершины, поэтому АО = 2см, а = 1см. Поэтому же ОД = х, а СО = 2х Медианы делят треугольник на 6 равновеликих (равных по площади) треугольников, поэтому площадь треугольника AOD S(AOD) = 1/6 S(ABC) = 12 : 6 = 2(см2) Площадь треугольника AOD можно вычислить и иначе: S(AOD) = 0.5 - AO OD - sin 30° = 0.5 - 2
x 0.5 = 0.5x
0.5x = 2 + = 4(см) - это OD, OC = 2x = 8(см) CD = OD + OC = 4 + 8 = 12(см) ответ: 12см