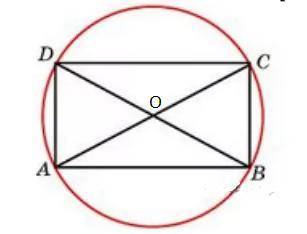
Стороны прямоугольника относятся как 4:3. Радиус окружности, описанной около прямоугольника, равен 10 см. Найдите стороны прямоугольника.
ОС - радиус нашей окружности. По условию равен 10 см.
АС - диаметр этой же окружности и соответственно он равен удвоенному радиусу:
AC = 2OC = 20 (см)
Рассмотрим треугольник АСD. Он прямоугольный. Так как АС - гипотенуза, пользуясь т.Пифагора и тем, что стороны прямоугольника относятся в отношении 4 : 3, составим уравнение.
Теорема Пифагора:
c² = a² + b² , где с - гипотенуза, а и b - катеты прямоугольного треугольника.
Тогда:
20² = (3x)² + (4x)²
400 = 9x² + 16x²
400 = 25x²
x² = 400 : 25
x² = 16
x = 4 и х = - 4 (не подходит по условию задачи)
Значит, стороны прямоугольника - 3 * 4 = 12 (см); 4 * 4 = 16 (см).
ответ: 12(см) и 16(см).
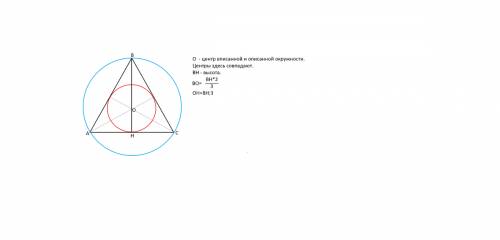
конус.
l (или РА, ВР) = 12 см
∠РВА = 30°
Найти:S осевого сечения - ?
Решение:Осевое сечение данного конуса (если секущая плоскость проходит через ось конуса) - равнобедренный треугольник, а высота Н (или РО) делит этот треугольник на два прямоугольных треугольника.
=> △ВРА - равнобедренный
=> △ВРО и △АРО - прямоугольные.
Рассмотрим △ВРО:
∠РВА = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> Н (или РО) = 12/2 = 6 см
Найдём радиус R (или ВО,ОА) по теореме Пифагора:
с² = а² + b²
b = √(c² - a²)
b = √(12² - 6²) = √(144 - 36) = √108 см
Итак, R (или ВО,ОА) = √108 см
Так как △ВРА - равнобедренный => △ВРО = △АРО (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △ВРА - равнобедренный)
Площадь прямоугольного треугольника равна полупроизведению его катетов:
=> S△АРО = ((√108) * 6)/2 = 18√3 см²
В равных треугольниках равные площади.
=> S△АРО = S△ВРО = 18√3 см²
=> S△ВРА = 18√3 + 18√3 = 36√3 см²
ответ: 36√3 см²