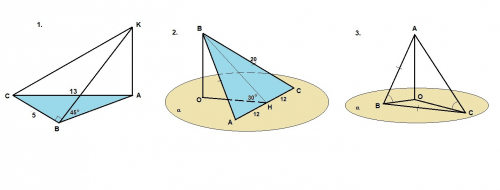
1. KA - перпендикуляр к плоскости треугольника ABC. Известно, КВ⊥BC.
а) докажите, что треугольник ABC - прямоугольный.
б) докажите, перпендикулярность плоскостей KAC и ABC.
в) найдите KA, если AC = 13 см, BC = 5 см, ∠KBA = 45°.
а) КВ - наклонная к плоскости ΔАВС, АВ - ее проекция, так как КВ⊥ВС, то и АВ⊥ВС по теореме, обратной теореме о трех перпендикулярах. Значит ΔАВС прямоугольный.
б) КА⊥(АВС), КА⊂(КАС), ⇒ (КАС)⊥(АВС), так как если плоскость проходит через прямую, перпендикулярную другой плоскости, то плоскости перпендикулярны.
в) Из прямоугольного треугольника АВС по теореме Пифагора:
АВ = √(АС² - ВС²) = √(13² - 5²) = √(169 - 25) = √144 = 12 см
ΔКАВ прямоугольный с углом 45°, значит равнобедренный,
КА = АВ = 12 см
2. ВО⊥α. ВО - искомое расстояние от точки В до плоскости α.
Пусть Н - середина АС. Треугольник АВС равнобедренный, значит ВН - медиана и высота треугольника.
ВН⊥АС, ОН - проекция ВН на плоскость α, значит ОН⊥АС по теореме, обратной теореме о трех перпендикулярах. Значит
∠ВНО = 30° - линейный угол двугранного угла между плоскостями АВС и α.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора:
ВН = √(АВ² - АН²) = √(20² - 12²) = √(400 - 144) = √256 = 16 см
ΔВОН: ∠ВОН = 90°,
ВО = ВН/2 = 8 см по свойству катета, лежащего напротив угла в 30°.
3. АО⊥α.
ОВ и ОС - проекции наклонных на плоскость α.
∠АВО = ∠АСО - углы, образованные наклонными с плоскостью α.
ΔАОВ = ΔАОС по катету и противолежащему острому углу (АО - общий катет, ∠АВО = ∠АСО по условию), значит
АВ = АС, а так как АВ = ВС по условию, то треугольник АВС равносторонний.
Углы ΔАВС равны 60°.
Прямоугольный параллелепипед .
.
 (см).
(см).
Найти: см.
см.
Решение:Квадрат диагонали нашего параллелепипеда равен сумме квадратов 3 его измерений: .
.
То есть из этого следует, что:
Остаётся найти объём по формуле, указанной выше:
 (см³).
(см³).
ответ: