ответ: угол А=50°
Объяснение: высота СН делит АВ на 2 прямоугольных треугольника АСН и ВСН. Рассмотрим полученный ∆ ВСН. В нём СН и ВН катеты, а СВ - гипотенуза.
Найдём угол В через синус угла.
Синус - это отношение противолежащего от угла катета к гипотенузе:
sinB=CH/CB=4/8=1/2=30°.
Итак: уголВ=30°. Сумма углов треугольника составляет 180°, поэтому
угол А=180-100-30=50°
Дано:
треугольник АМВ.
АМ = АВ = МВ.
DE = 6 см
Найти:
S от М до АВ
Так как МВ = АМ = АВ => треугольник АМВ - равносторонний.
А так как треугольник АМВ - равносторонний => этот треугольник ещё и равнобедренный.
Сумма углов треугольника равна 180°
∠А = ∠М = ∠В = 180°/3 = 60° (треугольник АМВ - равносторонний)
Так как треугольник АМВ - равнобедренный => MD - высота, медиана, биссектриса
=> ∠AMD = ∠BMD = 60˚/2 = 30˚
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> MD = 2DE
MD = 6 * 2 = 12 см
(MD - и есть расстояние от М до АВ)
ответ: 12 см.
Найдите объём шара, описанного около правильной четырёхугольной призмы со стороной основания 3 см и высотой √7 см
Объяснение:
V = 4/3* π* r³
В диагональном сечении данной комбинации тел получается прямоугольник , гипотенуза которого является диаметром шара.
В правильной четырёхугольной призмы основание-квадрат. По т. ПИфагора найдем диагональ основания :√(3²+3²)=√18 (см)..
Эта диагональ основания-сторона прямоугольника в диагональном сечении⇒ по т. Пифагора
d(призмы)=√( (√7)²+(√18)²)=√25=5 (см) ⇒ r=5/2 см
V = 4/3* π* (5/2)³=125π/6 (см³)
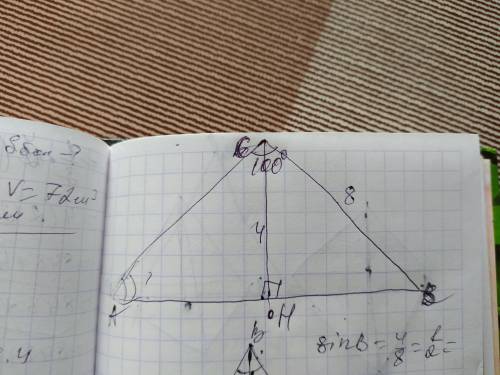
Дано: ΔABC, ∠С=100°, СН — высота, СН=4, СВ=8.
Найти: ∠САВ.
Решение.
1) В ΔBHC: ∠BHC=90°(т.к.СН — высота), СН=4, СВ=8.
В прямоугольном треугольнике, если катет равен половине гипотенузы, то угол против этого катета равен 30°.
СН=½СВ => ∠В= 30°.
2) В ΔABC:
Сумма углов треугольника равна 180°.
∠САВ+∠АВС+∠ВСА=180°;
∠САВ+30°+100°=180°;
∠САВ+130°=180°;
∠САВ=180°–130°;
∠САВ=50°.
ответ: 50°.