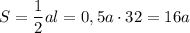
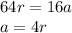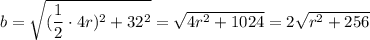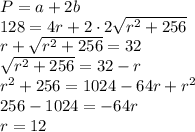
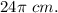
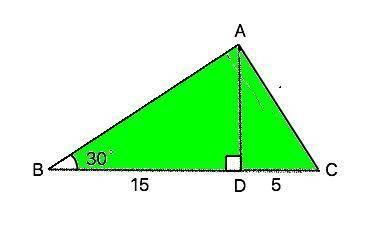
Высота АD треугольника ABC делит сторону BC на отрезки BD=15см и CD=5см,угол B=30°,AC-?

👇

Увидеть ответ

Ответ:

yanalitvinova

10.01.2021

Дано:

△АВС.

AD - высота.

BD = 15 см

CD = 5 см

∠В = 30°

Найти:

АС - ?

Решение:

Высота AD делит △АВС на два прямоугольных треугольника ABD и ACD.

Рассмотрим △ABD:

∠B = 30˚, по условию.

"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".

=> AD = 1/2AB

Составим уравнение:

Пусть х - AD, 2х - АВ, 15 - BD.

Теорема Пифагора:

с² = а² + b², где с - гипотенуза; a, b - катеты.

(2х)² = 15² + х²

4х² = 225 + х²

4х² - х² = 225

3х² = 225

х² = 75

х1 = 5√3

x2 = -5√3

Но так как единицы измерения не могут быть отрицательными => х = 5√3

Итак, AD = 5√3 см.

Найдём АС, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; a, b - катеты)

√((5√3)² + 5²) = √100 = 10 см

Итак, АС = 10 см

ответ: 10 см.

4,5(99 оценок)

Ответ:

Utugav

10.01.2021

Объяснение:

BD²=AB²-AD²

AD=x; AB=2x

15²=(2x)²-x²

225=3x²

x²=225÷3

x²=75

x=√75=5√3 см - AD

ΔCAD AC²=AD²+CD²

AC²=(5√3)²+5²

AC²=75+25=100

AC=√100=10 см

Высота АD треугольника ABC делит сторону BC на отрезки BD=15см и CD=5см,угол B=30°,AC-?

4,5(47 оценок)

Открыть все ответы

Ответ:

themac9

10.01.2021

Пусть h₁ - высота параллелограмма, a - его основание, b - основание равнобедренного треугольника, h₂ - высота равнобедренного треугольника, c - его боковая сторона.
Площадь параллелограмма равна произведению основания на высоту:
$S = h_{1}a = 5 \sqrt{6} a$
В равнобедренном треугольника высота, проведённая к основанию, является медианой и биссектрисой.
По теореме Пифагора (рассматривается треугольник, образованный высотой, а не весь равнобедренный треугольник):
$\dfrac{1}{2}b = \sqrt{c^2 - h_{2}^{2}} = \sqrt{7^2 - 5^2} = \sqrt{49 - 25} = \sqrt{24} = 2 \sqrt{6}$
Тогда $b = 4 \sqrt{6}$
Площадь треугольника равна половине произведения основания на высоту:
$S = \dfrac{1}{2}bh_{2} = \dfrac{1}{2} \cdot 4 \sqrt{6 } \cdot 5 = 10 \sqrt{6}$
Т.к. площади треугольника и параллелограмма равны, то
$5 \sqrt{6} a = 10 \sqrt{6} =\ \textgreater \ a = \dfrac{10 \sqrt{6} }{5 \sqrt{6} } = 2$
ответ: 2.

Высота параллелограмма имеет длину,равную 5 корень из 6. равнобедренный треугольник, боковая сторона

Высота параллелограмма имеет длину,равную 5 корень из 6. равнобедренный треугольник, боковая сторона

4,7(74 оценок)

Ответ:

ДианкаСафонова

10.01.2021

Пусть a - основание равнобедренного треугольника, l - биссектриса, r - радиус вписанной окружности, b - боковая сторона.
Выразим площадь треугольника через радиус вписанной окружности:
$S = \dfrac{1}{2}Pr = 0,5 \cdot 128r = 64r$
Биссектриса в равнобедренном треугольнике, проведённая к основанию, является и медианой, и высотой, поэтому:
$S = \dfrac{1}{2}al = 0,5a \cdot 32 = 16a$
Приравняем теперь обе формулы:
$64r = 16 a \\
a = 4r$ .
Найдём по теореме Пифагора боковую сторону b:
$b = \sqrt{( \dfrac{1}{2} \cdot 4r)^2 + 32^2} = \sqrt{4r^2 + 1024} = 2 \sqrt{r^2 + 256}$ .
У нас известен периметр, поэтому мы можем сложить все известные стороны и найти таким образом радиус вписанной окружности:
$P = a + 2b \\
128 = 4r + 2 \cdot 2 \sqrt{r^2 + 256} \\ 
r + \sqrt{r^2 + 256} = 32 \\ 
 \sqrt{r^2 + 256} = 32 - r \\ 
r^2 + 256 = 1024 - 64r + r^2 \\ 
256 - 1024 = -64r \\
r = 12$
Осталось найти длину круга:
$C = 2 \pi r = 24 \pi$
ответ: $24 \pi \ cm.$
Периметр равнобедренного треугольника=128 см, а биссектриса, проведенная к основе=32 см обчислите дл