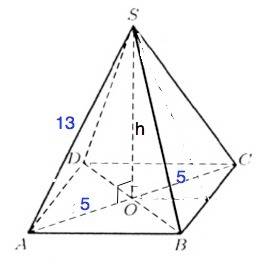
Диагональ основания правильной четырехугольной пирамиды равна 10 см, а боковое ребро 13 см. Найти площадь диагонального сечения пирамиды.
Основанием правильной четырехугольной пирамиды является квадрат, а вершина пирамиды проецируется в его центр, т.е. точку пересечения его диагоналей. .
Следовательно, высота ЅО принадлежит диагональному сечению АЅС пирамиды.
Пусть дана пирамида SABCD, SO -её высота. Диагонали основания равны, точкой пересечения делятся пополам, а диагональные сечения - равные равнобедренные треугольники.
Высота ЅО перпендикулярна основанию и любой прямой, на плоскости АВСD. =>
∆ АОЅ - прямоугольный.
По т.Пифагора ЅО=√(SA²-AO²)=√(169-25)=12см
S(ASC)=SO•AC:2=12•5=60 см²
Ромб.
AC = 16 см.
BD = 30 см.
Найти:AB - ?
Решение:"Ромб - параллелограмм, у которого все стороны равны".
=> АВ = ВС = СD = AD.
Так как ромб - параллелограмм, вспомним свойства параллелограмма:
"У параллелограмма диагонали точкой пересечения делятся пополам".
=> АЕ = ЕС = 16/2 = 8 см, DE = EB = 30/2 = 15 см.
Теперь, вспомним свойства ромба:
"Диагонали ромба взаимно перпендикулярны и делят его углы пополам".
=> △АЕВ, △АЕD, △CED, △CEB - прямоугольные.
Найдём стороны АВ, ВС, CD, AD, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
√(8² + 15²) = √(64 + 225) = √289 = 17 см.
Итак, АВ = ВС = CD = AD = 17 см.
ответ: 17 см.