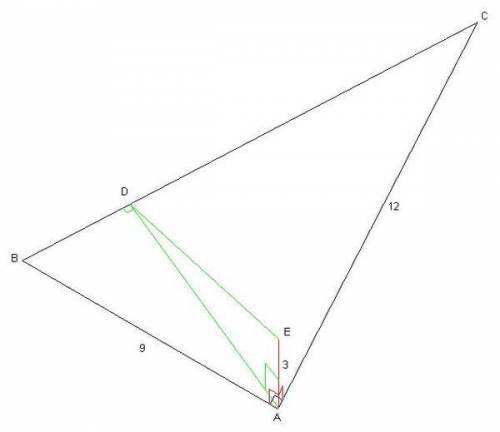
Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1.
Найдите длину отрезка ВВ1, если АС:СВ=4:3, СС1 = 8 см.
––––––––––
Через две параллельные прямые можно провести плоскость, притом только одну. ⇒
ВВ1 и СС1 лежат в одной плоскости.
Точки А, В, С. принадлежат отрезку АВ. ⇒ АВ ∈ той же плоскости.
Плоскость, проведенная через А, и плоскость, содержащая СС1 и ВВ1, пересекаются по прямой. АВ1.
Соответственные углы при параллельных прямых и секущей равны. ⇒
∠АСС1= ∠АВВ1, ∠АС1С=∠АВ1В ⇒
∆ АСС1~∆ АВВ1 по первому признаку подобия треугольников.
Пусть коэффициент отношения отрезков АС:ВС будет а.
Тогда АВ=7а
Из подобия следует отношение:
АВ:АС=ВВ1:СС1
7:4=ВВ1:8
4 ВВ1=56⇒
ВВ1=14
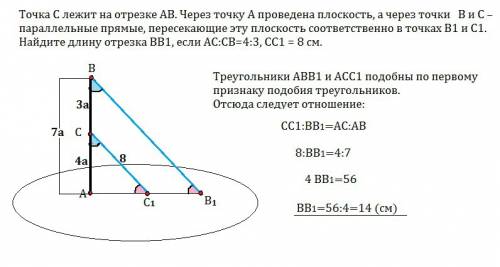
"Катеты прямоугольного треугольника равны 9см и 12см. В вершине прямого угла построен перпендикуляр к плоскости треугольника длиной 3см. Найти расстояния от концов перпендикуляра до гипотенузы. DA. это катет прямоугольного треугольника ADE. Второй катет известен, находишь гипотенузу DE."
Объяснение:
Расстоянием от А до СВ , будут АD, т.к АD⊥BС.
Расстоянием от Е до СВ , будут ЕD, т.к ЕD⊥BС по т. о трех перпендикуляра: если проекция АD перпендикулярна прямой лежащей в плоскости ВС, то и наклонная ЕD перпендикулярна ВС. .
1) ΔАВС-прямоугольный, по т. Пифагора СВ=√(9²+12²)=√225=15 (см).
По т. о среднем пропорциональном АС²=СD*СВ⇒ СD=144:15=9,6(см).
ΔАСD-прямоугольный , по т. Пифагора АD=√(12²-9,6²)=7,2 (см).
2)ΔАЕD-прямоугольный , по т. Пифагора ЕD=√(3²+7,2²)=7,8 (см).