Наверное вы имели в виду сумму длин всех рёбер паралделепипеда...
Значит, сумма длин всех ребер равна 180. Мы знаем, что в параллелепипеде 12 ребер, и он имеет 3 вида разных ребер. Из 12 ребер из каждого вида есть по 4 ребоа, что составляет в сумме 12.
Это можно покаазать вот так.
4х+4у+4а, а это равно 180
Можно в этом выражении 4 взять за скобки : 4*(х+у+а)=180.(сокращаем)
х+у+а=45
Видим,что их отношение
4:5:6 это отношение можно выразить как сумму переменных, т.е.
х+у+а=4с+5с+6с=45(сложим переменные)
15с=45
с=45:15
с=3
4с=12
5с=15
6с=18
Всё. Мы нашли размеры параллелепипеда.
Надеюсь все ясно
М∈АВ
N∈BC
P∈AC
И делит стороны так, что
MB=2AM, NC=2BN, AP=2PC, т.е. соотношение1:2
Отношение площадей треугольников имеющих равный (общий) угол равно произведению сторон содержащих этот угол. Доказательство этого факта приводить не буду. Желающие найдут (сделают :-) сами.
Рассмотрим, исходя из этого, треугольники АВС и AMP.
S(ABC)/S(AMP) = (AB*AC)/(AM*AP) (1)
Примем меньший отрезок АМ за 1 часть, соответственно MB будет 2 части.
Т.е. AB/AM = 3/1, AC/AP=3/2, подставим эти соотношения в выражение (1) для соотношения площадей треугольников получим:
S(ABC)/S(AMP) = (3*3)/(1*2) = 9/2, т.е. S(AMP)=(2/9)*S(ABC) =(2/9)*S
Можно провести аналогичные рассуждения для оставшихся треугольников, но учитывая соотношения сторон легко :-) заметить, что площади всех маленьких треугольников AMP, MBN, PNC равны и равны (2/9)*S.
Т.о. искомая площадь треугольника MNP будет равна
S-3*((2/9)*S) = 1/3 S, одной трети площади ABC, равной S.
И ещё. В чем смысл подобных задач? В том что ты учишься находить решение.
Сегодня это геометрия. Через годы это будут другие, более серьезные проблемы. На этом сайте ты научишься только списывать. Скачай себе
"Гордин-Планиметрия 7-9" и реши хотя бы одну задачу на соотношение площадей. Тогда я буду считать, что не зря потратил время, набивая всё это.
С тебя "69" :-)
Объяснение:
5)
Теорема Пифагора
KN=√(MN²-MK²)=√(25²-10²)=√(625-100)=
=√525=5√21
MK²=ME*MN
10²=ME*25
ME=100/25
ME=4
KN²=EN*MN
EN=KN²/MN
EN=525/25=21
KE²=EN*ME
KE=√(21*4)=√84=2√21
ответ: КЕ=2√21; EN=21; ME=4; KN=5√21
6)
KN=3x
KM=4x
Уравнение по теореме Пифагора.
КM²+KN²=NM²
9x²+16x²=50²
25x²=2500
x=√100
x=10
KN=3x=3*10=30
KM=4x=4*10=40
KN²=NF*NM
NF=KN²/NM=900/50=18
KM²=MF*NM
MF=KM²/NM=1600/50=32.
KF=√(FM*NF)=√(32*18)=24
ответ: КF=24; MF=32; NF=18; KM=40; KN=30
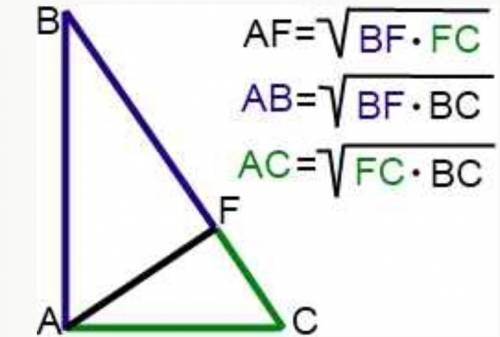
Формулы, которые использовались для нахождения необходимых значений на фото. А также применялась теорема Пифагора: - "Сумма квадратов катетов равна квадрату гипотенузы".
всего ребер 12 штук, пусть по возрастанию а, б, с, по условию
4*(а+б+с)=180см, а+б+с=45см, в долях 4+5+6=15, тогда 1 доля =45/15=3см, значит а=3*4=12см, б=3*5=15см, с=3*6=18см