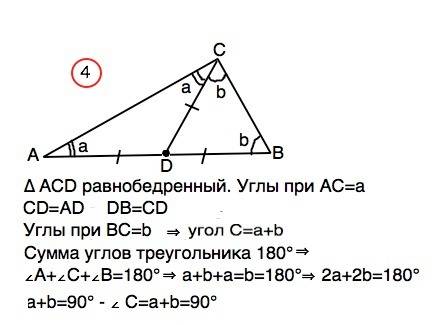
4) Примем угол А=а, угол В=b
В равнобедренном треугольнике углы при основании равны. ⇒
в ∆ АДС ∠АCD=∠CAD=а.
По условию СD=АD, а СD - медиана, и АD=ВD, ⇒ СD=ВD.
∆ ВDС равнобедренный. Углы при основании равнобедренного треугольника равны. ∠ВСD=∠СВD=b
Из найденного следует: угол С=а+b
Сумма углов треугольника 180°
Угол А+угол С+угол В=180° ⇒
а+b+a+b=180°
2a+2b=180°⇒
a+b=90° - угол С=а+b=90°
(Полезно помнить: Если в треугольнике медиана равна половине стороны, к которой проведена, этот треугольник – прямоугольный).
======
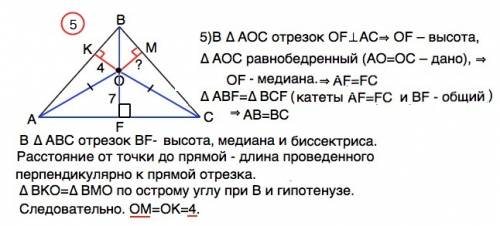
5) В ∆ АОС отрезок ОF перпендикулярен АС⇒ ОF – высота, а т.к. ∆ АОС равнобедренный (АО=ОС – дано), то ОF - медиана. ∆ АВF=∆ BCF– они прямоугольные с равными катетами: АF=FC (доказано), и ВF - общий, ⇒ АВ=ВС.
В равнобедренном ∆ АВС отрезок ВF- не только высота, но и медиана и биссектриса. Расстояние от точки до прямой - длина проведенного перпендикулярно к прямой отрезка.
Треугольники ВКО и ВМО прямоугольные с общей гипотенузой ВО и равным острым углом при В. Эти треугольники равны по углу и гипотенузе. Следовательно. ОМ=ОК=4.
≈≈≈≈≈≈≈≈
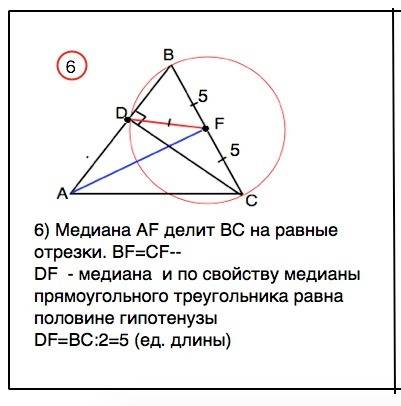
6) Медиана AF делит ВС на равные отрезки. BF=CF⇒
DF - медиана ∆ BDC и по свойству медианы прямоугольного треугольника равна половине гипотенузы
DF=ВС:2=5 (ед. длины)
======
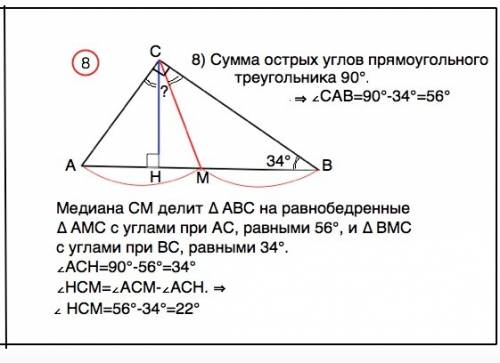
8) Сумма острых углов прямоугольного треугольника 90°. ⇒
угол САВ=90°-34°=56°
Медиана СМ делит ∆ АВС на равнобедренные: ∆ АМС с углами при АС, равными 56°, и ∆ ВМС с углами при ВС, равными 34°.
Угол АСН=90°-56°=34°
∠НСМ=∠АСМ -∠АСН.
Угол НСМ=56°-34°=22°
Вычислить расстояние между серединами отрезков MN и PQ. Даны координаты точек: M(1;2;1) N(3;-1;4)
P(-2;3:-3) Q(-4;-2;2)
Объяснение:
M(1;2;1) N(3;-1;4) . О-середина MN , найдем координаты О.
х(О)= ( х(M)+х(N) )/2 , х(О)= (1+3 )/2 , х(О)= 2 ; у(О)= ( у(M)+у(N) )/2 , у(О)= ( 2-1 )/2 , у(О)= 0,5;
z(О)= ( у(M)+у(N) )/2 , z(О)= ( 1+4 )/2 , z(О)= 2,5;
О( 2 ;0,5; 2,5) .
P(-2;3:-3) Q(-4;-2;2) , А-середина РQ , найдем координаты т A.
х(A)= ( х(P)+х(Q) )/2 , х(A)= (-2-4 )/2 , х(О)= -3 ; у(A)= ( у(P)+у(Q) )/2 , у(A)= ( 3-2 )/2 , у(О)= 0.5 ;
z(A)= ( у(P)+у(Q) )/2 , z(A)= ( -3-+2)/2 , z(О)= -0,5;
A( -3 ;0,5;-0,5) . .
ОА=√(-3-2)²+(0,5-0,5)²+(-0,5-2,5)²=√(25+0+9)=√34 .