Площади двух квадратов относятся как 9:4, а сумма их периметров 80 см. Найти сторону каждого из квадратов.
Объяснение:
Пусть сторона первого квадрата а см, тогда его S=a²,
а сторона второго квадрата в ,тогда его S=в².
Т.к. площади двух квадратов относятся как 9:4, то а²:в²=9:4.
Р(а)=4а, Р(в)=4в, 4а+4в=80 или а+в=20 или а=20-в.
а²:в²=9:4
(20-в)²:в²=9:4
(400-40в+в²) :в²=9:4 ( произведение крайних равно произведению средних)
9в²=4(400-40в+в²)
2,25в²=400-40в+в²
1,25в²+40в-400=0
Д=1600+2000=3600
в₁=-40 не подходит по смыслу задачи,
в₂=8 , поэтому а=20-8=12 (см)
ответ : 8 см, 12 см.
ответ:Сторона квадрату дорівнює 4см, а сторона рівновеликого йому прямокутника – 8см. Знайти другу сторону прямокутника.=35
Знайти площу ромба, сторона якого дорівнює 2√2 см, а один з його кутів дорівнює 45˚.=2,7
В прямокутному трикутнику висота, що проведена до гіпотенузи, ділить її
а відрізки 16см і 9см. Обчисліть площу трикутника.=8,14
В паралелограмі бісектриса гострого кута, який дорівнює 60˚, ділить сторону на відрізки 33см і 55см, починаючи від вершини тупого кута. Знайти площу і периметр паралелограму=7,4
Точка дотику кола, вписаного в рівнобічну трапецію, ділить бічну сторону у відношенні 9:4. Обчисліть периметр і площу трапеції, якщо довжина вписаного в неї кола дорівнює 24π см=0,7
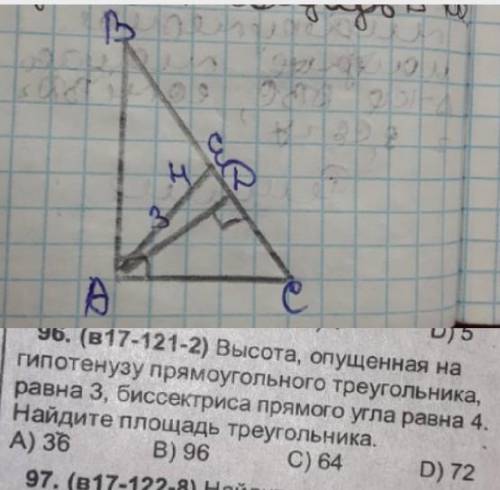
Высота, опущенная на гипотенузу прямоугольного треугольника, равна 3, биссектриса прямого угла равна 4. Найдите площадь треугольника.
ответ: 72 (ед. площади)
Объяснение:
∆ АВС, угол С=90°, высота СН =3, биссектриса СК=4.
Решение.
Из ⊿ СНК: sin ∠СКН=СН:СК=3/4=0,75 ⇒
∠СКН=48,59° - внешний ∆ АСК ⇒
∠САК=48,59°-∠АСК=48,59°-45=3,59°
∠СВА=90°-3,59°=86,4°
Из ⊿ АСН гипотенуза АС=СН:sinCAK=3:0,0626=47,9108
Из ⊿ СВН гипотенуза СВ=СН:sin CBH=3:0,998=3.006
Площадь прямоугольного треугольника равна половине произведения катетов.
S (ABC)=AC•BC=47,9108•3,006=72,009 ≈ 72 (ед. площади)