Сфера проходит через вершины квадраты АВСD, сторона которого равна 18см.
Радиус сферы ОD образует с плоскостью квадрата угол равный 60.
Найти:Расстояния от центра сферы – точки О до плоскости квадрата - ?
Решение:AB = 18 см.
ОО1 - расстояние от центра сферы О до плоскости квадрата ABCD.
Квадрат - геометрическая фигура, у которой все стороны равны ⇒ AB = BC = CD = AD = 18 см.
Проведём диагонали AC и BD квадрата ABCD.
О1 - точка пересечения диагоналей АС и BD.
Диагонали квадрата равны, делятся точкой пересечения пополам и взаимно перпендикулярны.
d = a√2, где d - диагональ квадрата; а - сторона квадрата.
d = AC = BD = 18√2 см.
⇒ AO1 = CO1 = DO1 = BO1 = 18√2/2 = 9√2 см.
∠OBO1 = 60˚.
tg (OBO1) = OO1/BO1 ⇒ OO1 = BO1 * tg (OBO1) = 9√2 * tg (60˚) = 9√2 * √3 = 9√6 см
ответ: 9√6 см.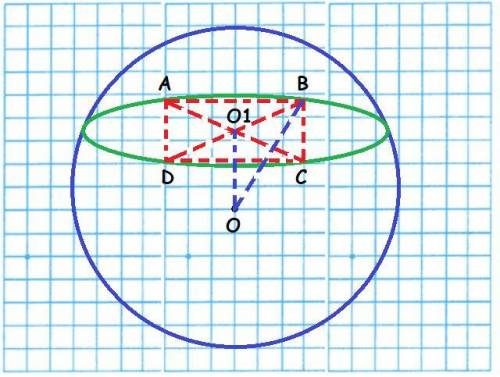
Прямые, соединяющие центр вписанной окружности с концами боковой стороны - это биссектрисы внутренних односторонних углов при параллельных основаниях и секущей боковой стороне. Сумма таких углов 180 градусов, сумма половин - 90 градусов, то есть эти прямые перпендикулярны. Поэтому радиус, проведенный в точку касания этой боковой стороны, является высотой к гипотенузе в прямоугольном треугольнике. Если меньший отрезок (на который точка касания делит гипотенузу-боковую сторону) принять за х, а больший за 4*х, то высота - среднее геометрическое этих отрезков.
Действительно, высота делит прямоугольный треугольник на два подобных между собой прямоугольных треугольника - и подобных исходному, конечно - по признаку равенства углов, поэтому
4*х/12 = 12/x;
(4*х)*х = 12^2 = 144; x^2 = 36; x = 6
Боковая сторона равна 30, а периметр 120
(сумма боковых сторон равна сумме оснований)
Трапеция АВСД. АВ=СД, точка М - касание на АВ, точка Л - касание на ВС, точка Р -касание на СД, точка Т -касание на АД
МВ/АМ=1/4, АМ=АТ как касательные проведенные из одной точки = ДК=ДР= 4 части угол А=уголД, ВМ=ВЛ=СЛ=СР = 1 части как касательные
АД = АТ+ДТ=4+4=8 частей
ВС=ВЛ+СЛ=1+1=2 части, проводим высоты ВН и СК на АД. треугольники АВН и КСД равны как прямоуголные треугольники по гипотенузе и острому углу уголА=уголД, АН=КД
четырехугольник НВСК - прямоугольник ВС=НК=2 части
АН=КД = (АД-НК)/2= (8-2)/2=3 части, АВ=АМ+ВМ=4+1=5 частей
Треугольник АВН, ВН=корень(АВ в квадрате - АН в квадрате) = корень(25-9) = 4 части
ВН=4 части = диаметру вписанной окружности = 2 х 12 =24
1 часть = 24/4=6
АВ = 5 х 6 = 30 =СД
ВС = 2 х 6 = 12
АД = 8 х 6 =48
Периметр = 30+30+12+48=120
Простите за качество фото
Объяснение: