54
Объяснение:
Площадь ромба равна половине произведения его диагоналей⇒ , где
, где
х-неизвестная диагональ.

Сумма углов треугольника 180°. Внешний угол треугольника равен сумме двух других, не смежных с ним.
Примем меньший внутренний угол равным х, тогда смежный внешний равен 5х. Их сумма равна градусной величине развернутого угла.
5х+х=180°⇒
х=30°
Случай 1:
Данный равнобедренный треугольник тупоугольный, тогда два его острых угла равны по 30°, третий из суммы углов треугольника равен 180°-2•30°=120°
Случай 2:
треугольник остроугольный. Меньший угол 30°, два других по
(180°-30°):2=75°
1) 30°, 30°, 120°
2) 30°, 75°, 75°
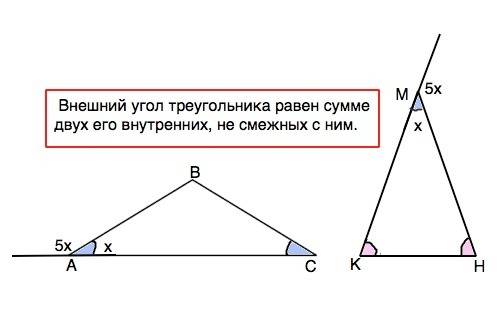
Сумма углов треугольника 180°. Внешний угол треугольника равен сумме двух других, не смежных с ним.
Примем меньший внутренний угол равным х, тогда смежный внешний равен 5х. Их сумма равна градусной величине развернутого угла.
5х+х=180°⇒
х=30°
Случай 1:
Данный равнобедренный треугольник тупоугольный, тогда два его острых угла равны по 30°, третий из суммы углов треугольника равен 180°-2•30°=120°
Случай 2:
треугольник остроугольный. Меньший угол 30°, два других по
(180°-30°):2=75°
1) 30°, 30°, 120°
2) 30°, 75°, 75°

Площадь ромба вычисляют по формуле:
S=1/2*d1*d2
Подставляем в формулу известное и находим неизвестное:
351=13*d2*1/2
1/2*d2=351/13
d2=27*2
d2=54