Дано : ΔABC остроугольный
AK ⊥ BC ; BD ⊥ AC ; AH =BC , H = AK ∩ BD ( H - точка пересечения высот)
∠BAC -?
ответ: 45° .
Объяснение:
Прямоугольные треугольники HDA и CDB равны ( третий признак равенства _ по гипотенузе и острому углу )
ΔHDA = ΔCDB
* * * ∠HDA = ∠BDC = 90 ° * * *
AH = BC ( гипотенузы по условию )
∠AHD =∠BCD углы со взаимно перпендикулярными сторонами : AH⊥ BC ; HD ⊥ AC (снова по условию) ,
следовательно AD = BD , т.е. прямоугольный треугольник ΔADB равнобедренный ⇒∠BAC = ∠ABC = 45° .
( ! Равенство второго пара катетов: HD = CD можно использовать при построения правильного чертежа. )
* * * Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны ( аналог второго признака равенства для "обычных "треугольников" ) * * *
* * * AK ⊥ BC ⇔ AH⊥ BC ; BD ⊥ AC ⇔ HD ⊥ AC ))) * * *
Дано : ΔABC остроугольный
AK ⊥ BC ; BD ⊥ AC ; AH =BC , H = AK ∩ BD ( H - точка пересечения высот)
∠BAC -?
ответ: 45° .
Объяснение:
Прямоугольные треугольники HDA и CDB равны ( третий признак равенства _ по гипотенузе и острому углу )
ΔHDA = ΔCDB
* * * ∠HDA = ∠BDC = 90 ° * * *
AH = BC ( гипотенузы по условию )
∠AHD =∠BCD углы со взаимно перпендикулярными сторонами : AH⊥ BC ; HD ⊥ AC (снова по условию) ,
следовательно AD = BD , т.е. прямоугольный треугольник ΔADB равнобедренный ⇒∠BAC = ∠ABC = 45° .
( ! Равенство второго пара катетов: HD = CD можно использовать при построения правильного чертежа. )
* * * Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны ( аналог второго признака равенства для "обычных "треугольников" ) * * *
* * * AK ⊥ BC ⇔ AH⊥ BC ; BD ⊥ AC ⇔ HD ⊥ AC ))) * * *
Объяснение:
Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
ΔМО₁С₁ -прямоугольный, tg∠МС₁О₁ =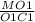
=
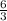⇒ tg∠МС₁О₁=2.