Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК= , AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
Средняя линия треугольника, соединяя середины двух любых сторон, всегда параллельна третьей стороне и равна 1/2 третьей стороны. В нашем случае OF - средняя линия треугольника ABC - то есть отрезок FO параллелен стороне AB и равен 1/2 AB. А отрезок FD равен стороне АВ, так как равен двум длинам отрезка FO (FO=FD) и параллелен стороне AB , так как лежит на средней линии. Таким образом мы имеем два параллельных, равных по длине отрезка AB и FD, что означает, что отрезки AD и BF тоже параллельны и равны по длине. Отсюда вывод : ABFD является параллелограммом.
1. СВ перпендикулярен пересечению АС двух перпендикулярных плоскостей ACD и ACB , значит любой отрезок в плоскости ACD является перпендикулярным CB (как принадлежащий плоскости, к которой СВ является перпендикуляром). То есть угол между СВ и любой прямой плоскости ACD является прямым, в том числе и угол DCB. Отсюда следует, что треугольник DCB - прямоугольный. 2. AH как перпендикуляр к плоскости АВСD перпендикулярен любой прямой на этой плоскости 3. Сначала найдём длину гипотенузы АС прямоугольного треугольника АВС с катетами 18 см. АС=√(18²+18²)=25,4558441... Отрезок АО является катетом прямоугольного треугольника АМО, он равен половине АС, то есть равен 25,4558441... : 2=12,7279220 Найдём гипотенузу АМ прямоугольного треугольника АОМ: АМ=√(12²+12,7279220²)=√(144+162)=17,492855 Но АМ является в свою очередь боковой стороной равнобедренного треугольника АВМ, основание которого равно 18 см. Таким образом мы можем вычислить площадь АВМ. Опустив высоту h из точки М на середину АВ равнобедренного треугольника АВМ, мы получим 2 прямоугольных треугольника, в которых данная высота будет катетом. h AMB=√((18/2)²+ 17,492855²)=√(81+306)=√387=19,67231... S ABM=(18×19,67231):2≈177 см² Причём в данной задаче я работал калькулятором, оперируя полными десятичными дробями без сокращений. Если принять высоту за округлённую до целого числа 20, то площадь получается 180 см², если округлить высоту до 19, получается 171 см². Но более точный результат - 177 см²
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК=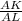 , AL=в / tgα.
, AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
3)ΔACК, угол ∠АСК=α.
По т. косинусов выразим cosα :
АК²=АС²+КС²-2АС*КС*cosα,
в²=2а²+а²+(а-в)²-2*а√2*√(а²+(а-в)²)*cosα,
2*а√2*√(а²+(а-в)²)*cosα =-в²+2а²+а²+(а-в)² ,
2*а√2*√(а²+(а-в)²)*cosα =-в²+4а²-2ав+в² ,
2*а√2*√(а²+(а-в)²)*cosα =2а(2а-в) ,
cosα =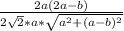
cosα =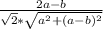 , tg²α=1:( cos²α)-1 , tgα =
, tg²α=1:( cos²α)-1 , tgα =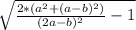 ,
,
tgα =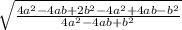 =
=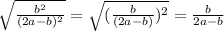
4)AL=в/tgα , AL=в: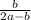 , AL=
, AL=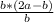 , AL=2a-b .
, AL=2a-b .