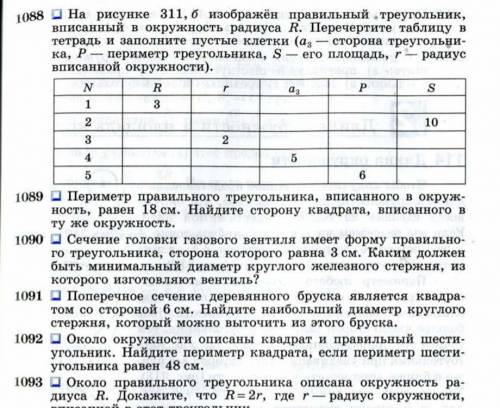
50, а проекция наклонной равна 6 см. Чему равна длина перпендикуляра, проведённого из этой же точки к плоскости?
4) Если прямая перпендикулярна двум радиусам круга, как она расположена по отношению к самому кругу?
5) Сколько можно провести прямых перпендикулярных данной прямой через данную точку, если а) эта точка лежит на прямой; б) эта точка не лежит на прямой?
6) Как между собой располагаются две прямые перпендикулярные одной и той же плоскости?
7) Могут ли перпендикуляр и наклонная, проведённые из одной и той же точки, иметь равные длины?
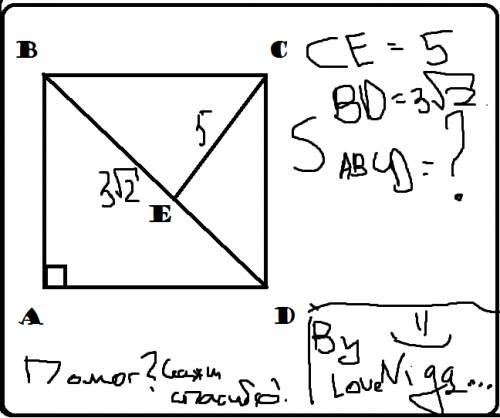
Из точки Е на ВС надо провести перпендикуляр. Пусть он пересекается с ВС в точке К. Тогда ВКЕ - равнобедренный прямоугольный треугольник, и его катеты ВК = ЕК = 3.
В прямоугольном треугольнике ЕКС катет ЕК = 3, гипотенуза ЕС = 5, то есть это "египетский" треугольник, его второй катет равен КС = 4.
Отсюда сторона квадрата ВС = 3 + 4 = 7, а площадь квадрата 7^2 = 49;
На самом деле, есть еще интересная возможность - если ЕD > BD. То есть точка E лежит на продолжении BD за точку B. В этом случае суть решения не меняется, но сторона квадрата ВС = 1, и площадь тоже 1.
Смотри вложение............................
Пояснение: у меня есть здоровская таблица - все вычисления выполнены с ей.