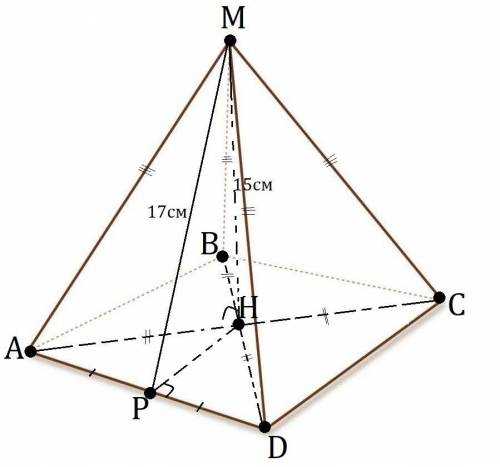
В правильной пирамиде высота падает в центр основания, то есть в центр правильного многоугольника. Правильный четырёхугольник это квадрат, а его центр находится на пересечении диагоналей. Боковые грани правильной пирамиды это равнобедренные треугольники, которые равны. Апофема это высота боковой грани. В квадрате все стороны равны, диагонали равны и делятся точкой пересечения пополам.
Пусть P∈AD и MP⊥AD, тогда MP=17см и AP=PD т.к. в равнобедренном Δ высота является и медианой.
Пусть H∈(ABC) и MH⊥(ABC), тогда AC∩BD=H.
ΔMHP - прямоугольный, найдём неизвестный катет.
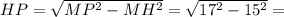
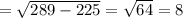 см.
см.
ΔAHD - равнобедренный, поэтому PH не только медиана, но и высота.
ΔHPD - прямоугольный, ∠HDP=45° т.к. диагонали квадрата являются и биссектрисами, значит HP=PD=8см - равны как катеты, прямоугольного Δ с острым углом в 45°.
AD=2·PD=2·8см=16см.
Площадь квадрата можно найти через сторону, а площадь равнобедренного треугольника через сторону и высоту опущенную на эту сторону.
S(ABCD) = AD²=16² см².
S(AMD) = MP·AD:2=17·16:2 см².
S(бок. пов.) = 4·S(AMD)=4·17·16:2 см²=2·17·16 см².
S(полн. пов.) = S(ABCD)+S(бок. пов.) = 16²см²+2·17·16 см² = 32·(8+17)см² = 8·4·25см²=800см².
ответ: 800см².
Проведём осевое диагональное сечение пирамиды.
В сечении имеем равнобокую трапецию.
Основания равны 10√2 и 14√2 см. Диагональ равна 18 см.
Проведём высоту из верхней точки на основание.
Проекция боковой стороны на основание равна (14√2- 10√2)/2 = 2√2.Оставшаяся часть нижнего основания равна 14√2 - 2√2 = 12√2.
Отсюда находим высоту пирамиды по Пифагору.
Н = √(18² - (12√2)²) = √(324 - 288) = √36 = 6 см.