Объяснение:
В прямоугольном треугольнике АВС угол С прямой,
катеты равны 15 см и 20 см.
Найдите косинус , синус и тангенс угла В.
Решение.
Косинус (cosB)- отношение прилежащего катета (ВС=20 см) к гипотенузе.
Находим гипотенузу по т. Пифагора
АВ²=АС²+ВС² = 15²+20²=225+400=625;
АВ = √625=25 см. Тогда
cosB = 20/25 = 4/5 = 0.8.
Cинус угла В (sinB) равен отношению противолежащего катета (AC=15 см) к гипотенузе (АВ=25 см)
sinB = 15/25 = 3/5 = 0,6.
Тангенс угла В (tgB) равен отношению противолежащего катета (AC=15 см) к прилежащему (ВС=20 см)
tgB =15/20 = 3/4 = 0.75.
10 см
Объяснение:
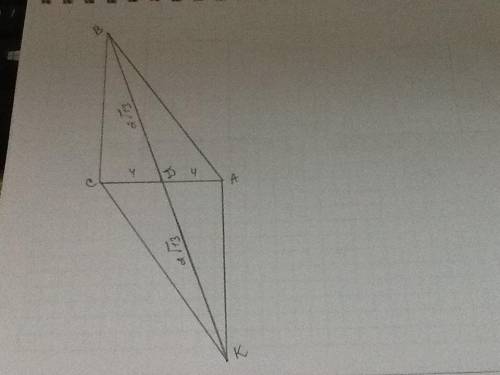
Дано: ΔАВС - прямоугольный, ∠С=90°, ВD - медиана, BD=2√13 cм, АС=8 см. АВ - ?
Если в условии дана медиана треугольника, я решаю задачу, достроив треугольник до параллелограмма. Теорема об удвоении медианы:
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Продлеваем медиану на такую же длину и строим параллелограмм АВСК, где диагональ АС=8 см, диагональ ВК=2√13+2√13=4√13 см.
Тогда АС²+ВК²=2(АВ²+ВС²).
208+64=2(АВ²+ВС²)
272=2(АВ²+ВС²)
АВ²+ВС²=136.
Вернемся к ΔАВС. По теореме Пифагора
АВ²+ВС²=136
АВ²-ВС²=64 (т.е. АС²)
2АВ² = 200; АВ²=100; АВ=10 см.
8 см
Объяснение:
Пусть дан треугольник АВС. АС=30см. Обозначим точки касания вписанной окружности и сторон треугольника АС, АВ и ВС соответственно К, Т, Р.
Тогда по условию задачи ВТ=12 см и АТ=14 см
Тогда АТ=АК= 14 см
КС= АС-АК=30-14=16 см
КС=РС=16 см
ВР=ВТ=12 см
Тогда АВ=АТ+ВТ=12+14=26 см, ВС =ВР+РС=12+16=28 см
Тогда периметр Р= 26+28+30=84 см
Тогда полупериметр р=Р:2=84:2=42
Тогда площадь треугольника по теореме Герона
S=sqrt(p*(p-a)*(p-b)*(p-c))= sqrt(42*12*14*16)=336
С другой стороны площадь треугольника может быть вычислена по формуле S=p*r=42*r=336
=> r=336/42
r=8