1. тупоугольный.
2. остроугольный.
3. прямоугольный.
Объяснение:Если 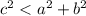 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - остроугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - остроугольный.
Если 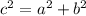 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - прямоугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - прямоугольный.
Если 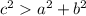 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - тупоугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - тупоугольный.
1. 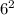 и
и 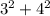
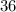 и
и 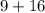
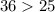
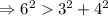 ⇒ данный треугольник - тупоугольный.
⇒ данный треугольник - тупоугольный.
2. 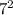 и
и 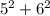
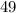 и
и 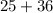
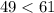
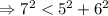 ⇒ данный треугольник - остроугольный.
⇒ данный треугольник - остроугольный.
3. 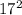 и
и 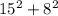
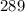 и
и 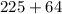
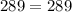
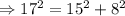 ⇒ данный треугольник - прямоугольный.
⇒ данный треугольник - прямоугольный.
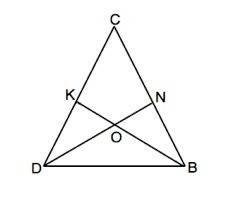
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.
К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.
Объяснение:
По условию 2АМ=МС. Пусть радиус окружности r. Нужно найти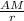 .
.
" Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB. "
АМ²=МВ*МС , но длина отрезка МВ=МС-2r ,
АМ²=( МС-2r)*2АМ |: АМ , МС=2АМ ,
АМ=(2АМ-2r)*2,
3АМ=4r ⇒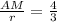 .
.