Геометрия: В шестиугольнике ABCDEF выполнены равенства FA >

В шестиугольнике ABCDEF выполнены равенства FA">

👇

Ответ:

ilya201296

02.09.2022

В шестиугольнике ABCDEF выполнены равенства FA=AB=BC=CD=DE, ∠A=100°, ∠B=140°, ∠C=110°, ∠D=130° . Найдите величину угла E.

ответ: ∠E = 105°.

Объяснение: ctg(α+β) =(ctgα*ctgβ -1) / (ctgα+ctgβ) ; ctgφ = √3 - 2 < 0 .

√3 -2 = (1 -√3)²/(-2) =(1 -√3 )²/(1+√3)(1 -√3)=(1 -√3)/(1+√3) =

(1 /√3 -1)/ (1 /√3 +1)=( ctg60°*ctg45° - 1) / (ctg60° +ctg45°) = ctg105° .

см вложение

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

ctg105 = (ctg60°*ctg45° - 1 ) / (ctg60° + ctg45°) =

(1/√3 - 1) / ( 1/√3 +1) = (1 -√3) / (1+√3 ) =

(1 -√3)² / (1+√3 )(1-√3) =(4-2√3)/(-2) =√3 -2.

В шестиугольнике ABCDEF выполнены равенства FA

4,4(66 оценок)

Открыть все ответы

Ответ:

mamarika2001

02.09.2022

а) Постройте плоскость, проходящую через точки K, L и М - для этого надо просто соединить эти точки.

б) Найдите угол между этой плоскостью и плоскостью основания АВС.
Продлим отрезки КМ и KL до пересечения с плоскостью АВС. Для этого достаточно продлить стороны АС и АВ.
Точки пресечения - это Д и Е.
Примем длину отрезка АК за 1.
Из треугольника АКД отрезок АД = 1 / tg 60 = 1 / √3.
Аналогично АЕ = 1 / tg 45 = = 1 / 1 = 1.
Угол ЕАД равен 60 градусов (по заданию).
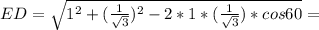
По теореме косинусов $ED= \sqrt{1^2+( \frac{1}{ \sqrt{3}} )^2-2*1*( \frac{1}{ \sqrt{3} } )*cos60}=$
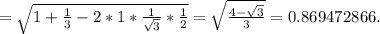
$= \sqrt{1+ \frac{1}{3} -2*1* \frac{1}{ \sqrt{3} }* \frac{1}{2}} = \sqrt{ \frac{4- \sqrt{3} }{3} } =0.869472866.
$
Находим гипотенузы в треугольниках АКД и АКЕ.
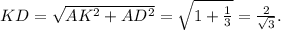
$KD= \sqrt{AK^2+AD^2} = \sqrt{1+ \frac{1}{3} } = \frac{2}{ \sqrt{3} } .$
КЕ = √(1²+1²) = √2 (острые углы по 45 градусов).
Теперь определены 3 стороны в треугольнике КЕД, угол наклона которого к плоскости АВС надо найти.
Для этого двугранный угол между основой и треугольником КДЕ надо рассечь плоскостью, перпендикулярной их линии пересечения ЕД.
Находим высоты в треугольниках АЕД и КЕД по формуле:
$h _{a} = \frac{2 \sqrt{p(p-a)(p-b)(p-c)} }{a} .$
АЕ ДЕ АД   p 2p S =
1   0.8694729    0.5773503   1.2234116   2.446823135     0.25
haе        hде      hад
0.5        0.57506   0.86603

КЕ    ДЕ   КД   p 2p S =
1.4142136 0.869473   1.154701   1.719194    3.43839   0.501492
hке    hде hкд
0.7092 1.15356   0.86861.
Отношение высот hде и  hде  - это косинус искомого угла:
cos α = 0.57506 / 1.15356 = 0.498510913.
ответ: α = 1.048916149 радиан = 60.09846842°.

4,7(87 оценок)

Ответ:

mukola11

02.09.2022

(МН·РН) = 4 ед.

(ОР·РК) = -2 ед.

Объяснение:

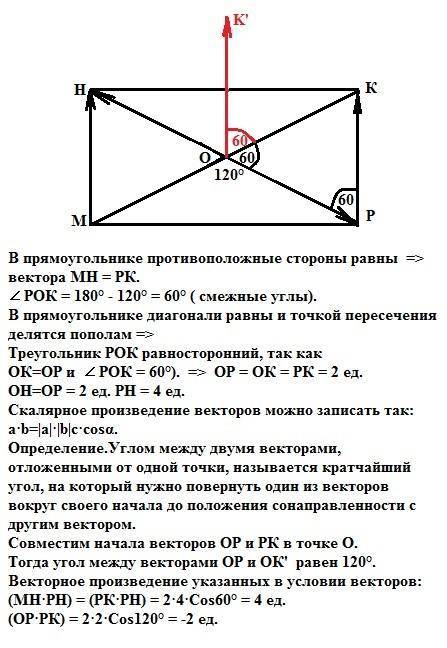
В прямоугольнике противоположные стороны равны =>

вектора МН = РК.

∠ РОК = 180° - 120° = 60° ( смежные углы).

В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>

Треугольник РОК равносторонний, так как

ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.

ОН=ОР = 2 ед. РН = 4 ед.

Скалярное произведение векторов можно записать так:

a·b=|a|·|b|c·сosα.

Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".

Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.

Векторное произведение указанных в условии векторов:

(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.

(ОР·РК) = 2·2·Cos120° = -2 ед.