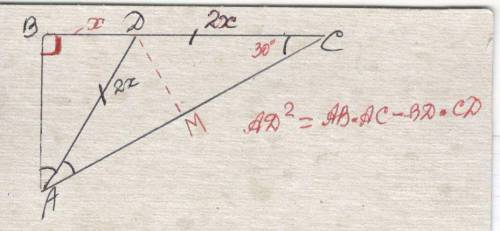
Дано : ΔABC; ∠BAD =∠CAD (AD → Биссектриса) ; AD=CD ; AC=2AB - - - - - - - - - - - - - -
∠ADB - ?
ответ: 60°
Объяснение: AD = CD ⇔ ∠С=∠CAD ; ∠ADB =∠С +∠CAD =2∠С ,
т.к. ∠ADB внешний угол ΔADC.
CD/BD =AC/AB (свойство биссектрисы)
СD/BD=2 ⇔ СD=2BD AD = CD = 2BD
! AD²= AB*AC - СD*BD ⇔ 4BD² =2AB² -2BD² ⇔3BD² =AB² ⇔
(2BD)²=AB²+BD² ⇔ AD²=AB²+BD² ⇒ ABD =90° (по обратной теореме Пифагора)
В ΔABC катет AB = половине гипотенузы AC ⇒ ∠С=30°
∠ADB =2∠С=60° . || ∠С = ∠A = 60° ; ∠B =90° ||
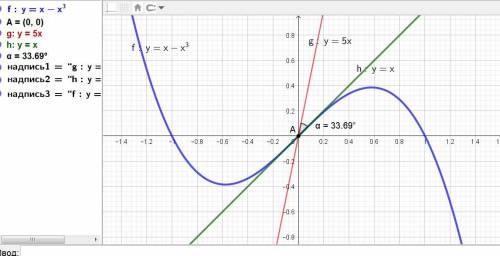
Даны кривая у = х - х^3 и прямая у = 5х
.
Находим их общую точку - точку пересечения.
Приравняем х - х^3 = 5х,
4x + х^3 = 0,
x(4 + x^2) = 0,
x = 0 один корень,
x^2 = -4 не имеет решения.
Угол между кривой и прямой равен углу между касательной к кривой и прямой.
Тангенс угла наклона касательной к оси Ох равен производной функции.
y' = 1 - 3x^2.
В точке х = 0 производная равна 1, то есть tg(fi) = 1.
Угол между прямыми находим по формуле:
tgα = (k2 - k1)/(1 + k2*k1) = (5 - 1)/(1 + 5*1) = 4/6 = 2/3.
α = arctg(2/3) = 0,5880 радиан или 33,690 градуса.
60°
Объяснение: