Объяснение:
а) Сперва доказываем что тр. АВС подобен тр. MNK по 1 признаку ( 2 угла равны)
Используя свойства подобных треугольников (стороны 1 тр. пропорциональны сторонам 2 тр. И имеют коэффициент k), находим сначала коэффициент k по известным нам сторонам BC и NK, а потом через коэффициент подобия (k) находим остальные стороны по пропорции, и в конце просто складываем.
b) Опять же сперва доказываем что тр. ABC подобен тр. MNK по первому признаку, и снова пользуясь свойством подобных треугольников, выражаем что : Pтр.ABC/Pтр.MNK = k ( коэффициенту подобия).
Находим k по известным нам сторонам, потом находим периметр тр. АВС, подставляем в формулу и просто решаем пропорцию. Надеюсь я


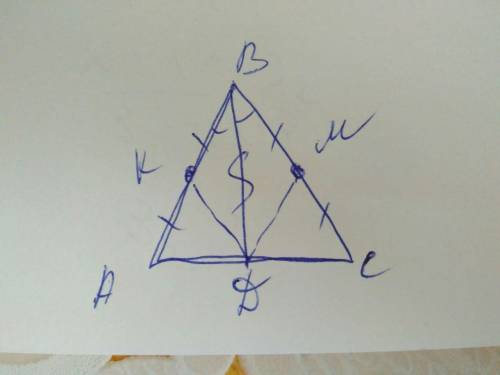
Дано: ΔАВС - равнобедренный, АК = КВ = ВМ = МС (т. К и М - середины боковых сорон АВ и СВ соответственно), ВD - медиана.
Доказать: ΔBKD = ΔBMD.
Доказательство: есть два треугольника BKD и BMD, у которых сторона BD - общая. стороны KB и BM - равны, т.к. ΔABC - равнобедренный, а точки K и M - середины сторон АВ и СВ соответственно. Т.к. BD - медиана равнобедренного ΔABC, то ∠KBD = ∠DBM. Следовательно, по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны), треугольники BKD и BMD равны, т.к. KB = BM, BD - общая сторона, ∠KBD = ∠DBM.
Чтд.
100
Объяснение:
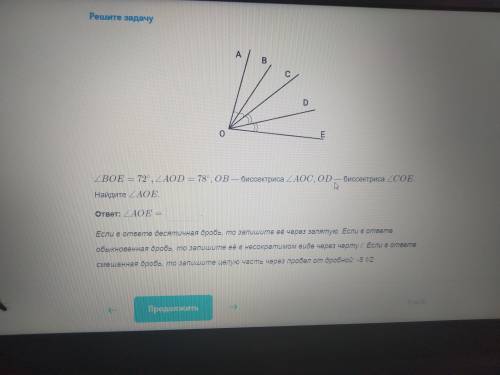
Пусть ∠COD=x, тогда ∠DOE=x
Пусть ∠AOB=y, тогда ∠BOC=y
Получим ∠BOE=2x+y
∠AOD=2y+x
2x+y=72
2y+x=78
y=72-2x, тогда 2(72-2x)+x=78
144-4x+x=78
3x=66
x=22 y=72-2*22=72-44=28
∠AOE=2x+2y=2(x+y)=2(22+28)=100