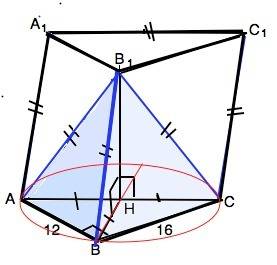
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
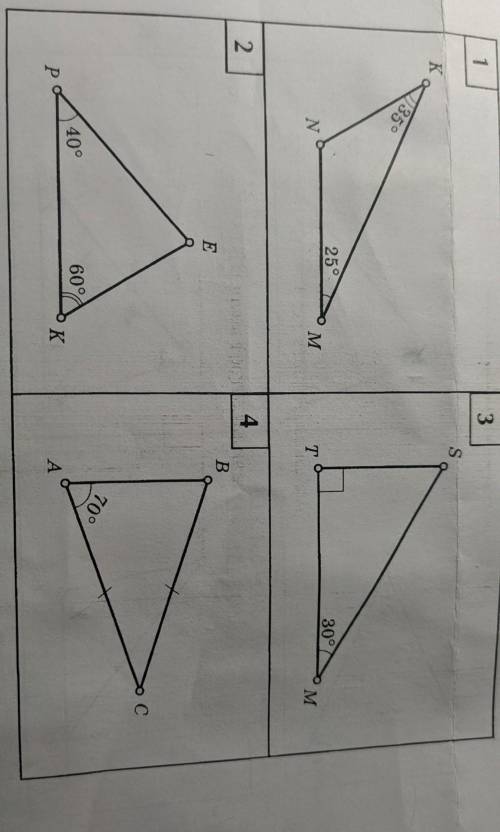
1)120°;
2)80°;
3)60°;
4)40°
Пользуемся теоремой о сумме 3-х углов треугольника и решаем
1)∠К+∠M+∠N=180°;0°
∠N=180°-(∠К+∠M)=180°-(35°+25°)=180°-60°=120°
2)∠E+∠P+∠K=180°;
∠E=180°-∠P-∠K=180°-60°-40°=80°
3) Как следствие теоремы для прямоугольных треугольников ( Сума острых углов в прямоугольном треугольнике равна 90°)
∠S+∠M=90°;
∠S=90°-30°=60°.
4)Тут используем свойство равнобедренного треугольника: Если треугольник является равнобедренным треугольником, то углы при его основании равны.
∠А=∠В=70°
∠С=180-2*70°=40°